
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:不详 题型:解答题
 .
. ,求
,求 的概率分布及数学期望.
的概率分布及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示取出的3张卡片的最大数字,求:
表示取出的3张卡片的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望; ,求
,求 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的等比数列,第一项测试合格且第二项测试也合格的概率为
的等比数列,第一项测试合格且第二项测试也合格的概率为 .
.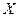 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为
.设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为 ,对该项目每投资十万元,
,对该项目每投资十万元, 取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
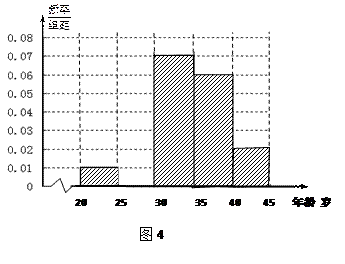
 岁的人数(结果取整数);
岁的人数(结果取整数);| 分组 (单位:岁) | 频数 | 频率 |
 | 5 | 0.050 |
 | ① | 0.200 |
 | 35 | ② |
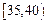 | 30 | 0.300 |
 | 10 | 0.100 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com