
【题目】某校举行运动会,其中三级跳远的成绩在![]() 米以上的进入决赛,把所得的数据进行整理后,分成
米以上的进入决赛,把所得的数据进行整理后,分成![]() 组画出频率分布直方图的一部分(如图),已知第
组画出频率分布直方图的一部分(如图),已知第![]() 组的频数是
组的频数是![]() .
.
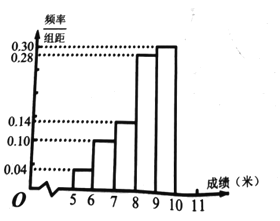
(1)求进入决赛的人数;
(2)经过多次测试后发现,甲的成绩均匀分布在![]() 米之间,乙的成绩均匀分布在
米之间,乙的成绩均匀分布在![]() 米之间,现甲、乙各跳一次,求甲比乙远的概率.
米之间,现甲、乙各跳一次,求甲比乙远的概率.
科目:高中数学 来源: 题型:
【题目】图①中△ABC 为直角三角形![]() D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
D、E 分别为 AB、AC 的中点,将△ADE 沿 DE 折起使平面 ADE⊥BCED,连接 AB,AC,BE如图②所示.
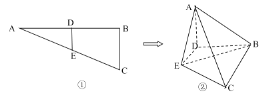
(1)在线段AC上找一点P,使EP∥平面ABD,并求出异面直线AB、EP所成的角;
(2)在平面ABD内找一点Q,使PQ⊥平面ABE,并求三棱锥P-ABE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() .
.
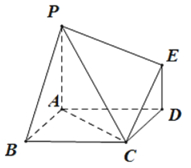
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为45°,求平面
所成的角为45°,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求实数
,若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是圆锥的顶点,BD是圆锥底面的直径,C是底面圆周上一点,AC=BD=2,BC=1,点M在线段BD上,且BM![]() ,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
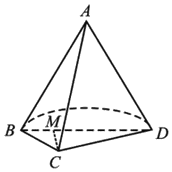
(1)求证:CM⊥AD;
(2)求AC与底面所成的角;
(3)求该几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤梨穗龙眼原产厦门,是厦门市的名果,栽培历史已有100多年.龙眼干的级别按直径![]() 的大小分为四个等级(如下表).
的大小分为四个等级(如下表).
|
|
|
|
|
级别 | 三级品 | 二级品 | 一级品 | 特级品 |
某商家为了解某农场一批龙眼干的质量情况,随机抽取了100个龙眼干作为样本(直径分布在区间![]() ),统计得到这些龙眼干的直径的频数分布表如下:
),统计得到这些龙眼干的直径的频数分布表如下:
|
|
|
|
|
|
频数 | 1 |
| 29 |
| 7 |
用分层抽样的方法从样本的一级品和特级品中抽取6个,其中一级品有2个.
(1)求![]() 、
、![]() 的值,并估计这批龙眼干中特级品的比例;
的值,并估计这批龙眼干中特级品的比例;
(2)已知样本中的100个龙眼干约500克,该农场有500千克龙眼干待出售,商家提出两种收购方案:
方案![]() :以60元/千克收购;
:以60元/千克收购;
方案![]() :以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
:以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
用样本的频率分布估计总体分布,哪个方案农场的收益更高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)满足:集合A={f(n)|n∈N*}中至少有三个不同的数成等差数列,则称函数f(x)是“等差源函数”,则下列四个函数中,“等差源函数”的个数是( )
①y=2x+1;②y=log2x;③y=2x+1;
④y=sin![]()
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com