
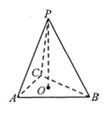
����Ŀ��2019��4��10��21ʱ����ȫ�����أ��Ϻ���̨������³������ʥ���Ǹ硢�����ͻ�ʢ��ͬʱ�ٿ����ŷ����ᣬ���������״��������������Զ�����ɹ��������������źڶ�ͼ��������Ƭչʾ��һ������Ϊ��ɫ��������״�ṹ������ȥ�е������ɫ������Ȧ�����ɫ�����Ǻڶ�Ͷ�µġ���Ӱ���������������ƺڶ�������ת��������.ijͬѧ����һ�źڶ�ʾ��ͼ����ͼ��ʾ��������ͬ��Բ�Ͱ��ͬ��Բ������Բ��Բ���İ뾶���ڵ�������Ϊ2��3��4��5����λ��ͼ�������ȡһ�㣬��õ�ȡ����Ӱ�ĸ���Ϊ�� ��
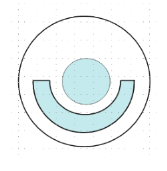
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ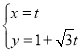 ��
��![]() Ϊ��������������ԭ��Ϊ���㣬��
Ϊ��������������ԭ��Ϊ���㣬��![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() .
.
��1����ֱ��![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ԫ����ɵļ���![]() ��
��![]() ���Ǽ���
���Ǽ���![]() �е�Ԫ�ظ���Ϊ
�е�Ԫ�ظ���Ϊ![]() ����
����![]() .����
.����![]() ������
������![]() �е�Ԫ�ظ�����Ϊ
�е�Ԫ�ظ�����Ϊ![]() ����
����![]() ʱ���Ƽ���
ʱ���Ƽ���![]() ��������
��������![]() .
.
��1��![]() ��
��![]() ���жϼ���
���жϼ���![]() ��
��![]() �Ƿ��������
�Ƿ��������![]() ����˵�����ɣ�
����˵�����ɣ�
��2���輯��![]() ��
��![]() ��
��![]() (
(![]() )��������
)��������![]() ��������
��������![]() ����
����![]() �����ֵ��
�����ֵ��
��3���輯��![]() ����������
����������![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�![]() (
(![]() )�ҹ���Ϊ���������жϼ���
)�ҹ���Ϊ���������жϼ���![]() �Ƿ��������
�Ƿ��������![]() ��˵������.
��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ�����ڳ�Ϊ1ǧ�����ɵ�![]() һ���һƬ��������ʱ�һ��ǿ���ƻ���У��ѯ������̨����������ֱ������������
һ���һƬ��������ʱ�һ��ǿ���ƻ���У��ѯ������̨����������ֱ������������![]() ��
��![]() Ϊֱ�ǣ�����
Ϊֱ�ǣ�����![]() Ϊֱ���İ�Բ��������ɣ���
Ϊֱ���İ�Բ��������ɣ���![]() ������
������![]() ��
��![]() ��Ϊ��Բ����һ�㣬��
��Ϊ��Բ����һ�㣬��![]() ���߶�
���߶�![]() �ϣ�������
�ϣ�������![]() .��֪
.��֪![]() ����
����![]() ����
����![]() .�����������ѯ̨�������߶�
.�����������ѯ̨�������߶�![]() ��
��![]() �ϣ����������������ڻ�
�ϣ����������������ڻ�![]() ���߶�
���߶�![]() ��.
��.
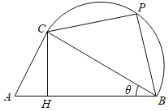
��1����Ϊ����ѧ����ø������ѯ���ᣬ�ø����ʡ�ڸ�У��չ��������![]() ���������ֵ��
���������ֵ��
��2����Ϊ����ѧ���˽�����ʡ���У�����������У�ĺ����������û�![]() ���߶�
���߶�![]() �ij���֮��������ʱ��
�ij���֮��������ʱ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֽ��һ�������������۳��ܶ���ѧͼ�Σ���һ��Բ��ֽƬ����ƽ��ֱ������ϵ�У�Բ��B����1��0�����뾶Ϊ4��Բ��һ��AΪ������![]() �Ľ��㣮��ÿ�ν�ֽƬ����һ�ǣ�ʹ���ֵ�Բ����һ��
�Ľ��㣮��ÿ�ν�ֽƬ����һ�ǣ�ʹ���ֵ�Բ����һ��![]() ʼ�����A�غϣ���ֽչƽ���õ�һ���ۺۣ����ۺ����߶�
ʼ�����A�غϣ���ֽչƽ���õ�һ���ۺۣ����ۺ����߶�![]() B�Ľ���ΪP��
B�Ľ���ΪP��
����ֽƬչƽ�����P�Ĺ켣C�ķ��̣�
������֪����A��ֱ��l��켣C����R��S���㣬��l������α䶯����AB����ֱ���ϴ���һ��T��ʹ��![]() ����ֱ��һ������ԭ�㣬���T�����꣮
����ֱ��һ������ԭ�㣬���T�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫ����һ�뾶Ϊ![]() ��Բ��ֽƬ���������ΰ�װ��.��֪��ֽƬ��Բ��Ϊ
��Բ��ֽƬ���������ΰ�װ��.��֪��ֽƬ��Բ��Ϊ![]() ������
������![]() Ϊ�������߳�Ϊ
Ϊ�������߳�Ϊ![]() ����λ��
����λ��![]() ���ĵȱ�������
���ĵȱ�������![]() ���ٷֱ���Բ
���ٷֱ���Բ![]() ��ȡ������
��ȡ������![]() ��
��![]() ��
��![]() ��ʹ
��ʹ![]() ��
��![]() ��
��![]() �ֱ�����
�ֱ�����![]() ��
��![]() ��
��![]() Ϊ�ױߵĵ���������.���������ֱ���
Ϊ�ױߵĵ���������.���������ֱ���![]() ��
��![]() ��
��![]() Ϊ�ۺ�����
Ϊ�ۺ�����![]() ��
��![]() ��
��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() �غ��ڵ�
�غ��ڵ�![]() �����ɵõ�������
�����ɵõ�������![]() .
.
��1��������![]() ���������壬��
���������壬��![]() ��ֵ��
��ֵ��
��2��������![]() �����
�����![]() �����ֵ����ָ����Ӧ
�����ֵ����ָ����Ӧ![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn��a1��1��an��0��Sn2��an+12����Sn+1��������Ϊ����.
��1��֤����Sn+1��2Sn+����
��2���Ƿ����ʵ������ʹ������{an}Ϊ�ȱ����У������ڣ���������������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
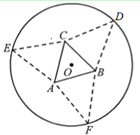
����Ŀ����֪Բ![]() ��Բ
��Բ![]() ����ͼ��
����ͼ��![]() �ֱ�
�ֱ�![]() ���������ڵ�
���������ڵ�![]() .����
.����![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ������
������![]() ����ֱ��
����ֱ��![]() ��
��![]() �ᴹֱ��ֱ��
�ᴹֱ��ֱ��![]() ��
��![]() �ᴹֱ.
�ᴹֱ.
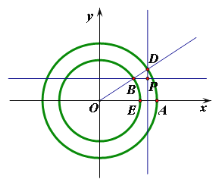
��1����![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ��
��ֱ��![]() ������
������![]() ���
���![]() ������
������![]() ���
���![]() ���ҽ�����
���ҽ�����![]() �ڵ�
�ڵ�![]() .�ʣ�
.�ʣ�![]() ��ֵ�Ƿ��Ƕ�ֵ������Ƕ�ֵ��������ö�ֵ��������Ƕ�ֵ����˵������.
��ֵ�Ƿ��Ƕ�ֵ������Ƕ�ֵ��������ö�ֵ��������Ƕ�ֵ����˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com