
分析 ①由于A,B在抛物线上,根据抛物线的定义可知A'F=AF,B'F=BF,从而由相等的角,由此可判断A'F⊥B'F;
②取AB中点C,利用中位线即抛物线的定义可得CM=$\frac{1}{2}(AF+BF)=\frac{1}{2}AB$,从而AM⊥BM;
③由②知,AM平分∠A′AF,从而可得A′F⊥AM,根据AM⊥BM,利用垂直于同一直线的两条直线平行,可得结论;
④取AB⊥x轴,则四边形AFMA'为矩形,则可得结论;
⑤取AB⊥x轴,则四边形ABB'A'为矩形,则可得结论.
解答 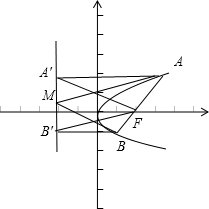 解:①由于A,B在抛物线上,根据抛物线的定义可知A'A=AF,B'B=BF,因为A′、B′分别为A、B在l上的射影,所以A'F⊥B'F;
解:①由于A,B在抛物线上,根据抛物线的定义可知A'A=AF,B'B=BF,因为A′、B′分别为A、B在l上的射影,所以A'F⊥B'F;
②取AB中点C,则CM=$\frac{1}{2}(AF+BF)=\frac{1}{2}AB$,∴AM⊥BM;
③由②知,AM平分∠A′AF,∴A′F⊥AM,∵AM⊥BM,∴A'F∥BM;
④取AB⊥x轴,则四边形AFMA′为矩形,则可知A'F与AM的交点在y轴上;
⑤取AB⊥x轴,则四边形ABB'A'为矩形,则可知AB'与A'B交于原点
故答案为①②③④⑤.
点评 本题以抛物线为载体,考查抛物线的性质,解题的关键是合理运用抛物线的定义.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
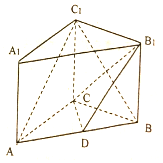 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a、b、c中至少有二个为负数 | B. | a、b、c中至多有一个为负数 | ||
| C. | a、b、c中至多有二个为正数 | D. | a、b、c中至多有二个为负数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.
已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-$\sqrt{3}$x+2 | B. | y=-$\sqrt{3}$x-2 | C. | y=$\sqrt{3}$x+2 | D. | y=$\sqrt{3}$x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
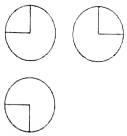 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com