练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在中，，是内切圆圆心，设是⊙外的三角形区域内的动点，若，则点所在区域的面积为    ▲       

     

    【答案】

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，在三棱锥S-ABC中，侧面SAB⊥底面ABC，且∠ASB=∠ABC=90°，AS=SB=2，AC=2
    		3
    ．

    （Ⅰ）求证SA⊥SC；
    （Ⅱ）在平面几何中，推导三角形内切圆的半径公式r=
    2S
    l
    （其中l是三角形的周长，S是三角形的面积），常用如下方法（如右图）：
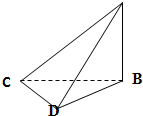    ①以内切圆的圆心O为顶点，将三角形ABC分割成三个小三角形：△OAB，△OAC，△OB精英家教网C．
    ②设△ABC三边长分别为a，b，c．由S△ABC=S△OBC+S△OAC+S△OAB，
    得S=
    1
    2
    ar+
    1
    2
    br+
    1
    2
    cr    =
    1
    2
    lr    ，则r=
    2S
    l
    ．
    类比上述方法，请给出四面体内切球半径的计算公式（不要求说明类比过程），并利用该公式求出三棱锥S-ABC内切球的半径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在Rt△ABC中，∠C=90°，AC=BC=2，D是△ABC内切圆圆心，设P是⊙D外的三角形ABC区域内的动点，若
    CP
    =λ
    CA
    +μ
    CB
    ，则点（λ，μ）所在区域的面积为
    1
    2
    -（
    3
    2
    -
    		2
    ）π
    1
    2
    -（
    3
    2
    -
    		2
    ）π
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网给出以下判断：
    （1）b=0是函数f（x）=ax2+bx+c为偶函数的充要条件；
    （2）椭圆
    x2
    4
    +
    y2
    3
    =1    中，以点（1，1）为中点的弦所在直线方程为x+2y-3=0；
    （3）回归直线
    y
    =
    b
    x+
    a
     必过点(
    .
    x
    ，
    .
    y
    )    ；
    （4）如图，在四面体ABCD中，设E为△BCD的重心，则
    AE
    =
    AB
    +
    1
    2
    AC
    +
    2
    3
    AD
    ；
    （5）双曲线
    x2
    a2
    -
    y2
    b2
    =1( a＞0 ， b＞0 )    的两焦点为F1，F2，P为右支是异于右顶点的任一点，△PF1F2的内切圆圆心为T，则点T的横坐标为a．其中正确命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年福建省高二下学期学段考试数学理卷 题型：选择题

    由“在平面内三角形的内切圆的圆心到三边的距离相等”联想到“在空间中内切于三棱锥的球的球心到三棱锥四个面的距离相等”这一推理过程是   （    ）

    A、归纳推理  B、类比推理  C、演绎推理  D、联想推理

     

    查看答案和解析>>

    同步练习册答案