
【题目】已知![]() ,设曲线
,设曲线![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)求函数![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(1)增区间为![]() ,减区间为
,减区间为![]() ;(2)当
;(2)当![]() 时,
时,![]() 的最小值为a;当
的最小值为a;当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)先求得![]() 的定义域,然后利用导数求得
的定义域,然后利用导数求得![]() 的单调区间.
的单调区间.
(2)根据![]() 在区间
在区间![]() 的左侧、内部、右侧进行分类讨论
的左侧、内部、右侧进行分类讨论![]() 的单调性,由此求得
的单调性,由此求得![]() 在区间
在区间![]() 上的最小值.
上的最小值.
(1)函数的定义域为![]() ,
,
![]() ,由
,由![]() 得
得![]() ,
,
所以列表如下
|
|
|
|
| 大于0 | 0 | 小于0 |
| 增函数 | 极大值 | 减函数 |
所以函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
(2)由上面的推理得函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,
需要对![]() 在区间
在区间![]() 的左侧、内部、右侧进行分类讨论,如下:
的左侧、内部、右侧进行分类讨论,如下:
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() 的最小值为
的最小值为![]() ;
;
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() 的最小值为
的最小值为![]() ;
;
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]() 的最小值为
的最小值为![]() ,
,![]() 中的较小者,故当
中的较小者,故当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
综上所述,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;.
;.
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求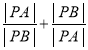 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用字母![]() 表示.我们可以通过设计一个试验来估计
表示.我们可以通过设计一个试验来估计![]() 的值:从
的值:从![]() 表示的区域内随机抽取200个实数对
表示的区域内随机抽取200个实数对![]() ,其中x,y两个数能与1构成钝角三角形三边长的数对
,其中x,y两个数能与1构成钝角三角形三边长的数对![]() 共有56个.则用随机模拟的方法估计
共有56个.则用随机模拟的方法估计![]() 的近似值为________.
的近似值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民用天然气实行阶梯价格制度,具体见下表:
阶梯 | 年用气量(立方米) | 价格(元/立方米) |
第一阶梯 | 不超过228的部分 | 3.25 |
第二阶梯 | 超过228而不超过348的部分 | 3.83 |
第三阶梯 | 超过348的部分 | 4.70 |
从该市随机抽取10户(一套住宅为一户)同一年的天然气使用情况,得到统计表如下:
居民用气编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年用气量(立方米) | 95 | 106 | 112 | 161 | 210 | 227 | 256 | 313 | 325 | 457 |
(1)求一户居民年用气费y(元)关于年用气量x(立方米)的函数关系式;
(2)现要在这10户家庭中任意抽取3户,求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望;
(3)若以表中抽到的10户作为样本估计全市居民的年用气情况,现从全市中依次抽取10户,其中恰有k户年用气量不超过228立方米的概率为![]() ,求
,求![]() 取最大值时的值.
取最大值时的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:参数方程选讲]
在直角坐标系xoy中,曲线![]() 的参数方程是
的参数方程是 (t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
(t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两曲线交点为A、B,求![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com