
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
分析 根据三角函数的图象和性质,可得命题p:a=1+4k,k∈Z;根据直线与圆的位置关系,可得命题q:a=1,或a=9,进而根据充要条件的定义,可得答案.
解答 解:当$\frac{π}{2}x$=$\frac{π}{2}$+2kπ,k∈Z,即x=1+4k,k∈Z时,函数$y=sin\frac{π}{2}x$取到最大值;
故命题p:a=1+4k,k∈Z;
若直线x-y+2=0与圆(x-3)2+(y-a)2=8相切,
则$\frac{|3-a+2|}{\sqrt{2}}$=2$\sqrt{2}$,
解得:a=1,或a=9,
即命题q:a=1,或a=9,
故p是q的必要不充分条件,
故选:B
点评 本题考查的知识点是充要条件的定义,函数的最值及其几何意义,直线与圆的位置关系,难度中档.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | 3-i | B. | 1+3i | C. | 3+i | D. | 1-3i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
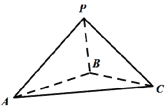 如图所示,四面体P-ABC中,$∠APB=∠BPC=∠CPA=\frac{π}{2}$,PA=4,PB=2,$PC=\sqrt{5}$,则四面体P-ABC的外接球的表面积为25π.
如图所示,四面体P-ABC中,$∠APB=∠BPC=∠CPA=\frac{π}{2}$,PA=4,PB=2,$PC=\sqrt{5}$,则四面体P-ABC的外接球的表面积为25π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{-1+\sqrt{3}}}{2}$ | B. | $\frac{{-1+\sqrt{5}}}{2}$ | C. | $\frac{{1+\sqrt{5}}}{2}$ | D. | $2+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
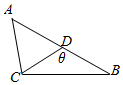 △ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.
△ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com