
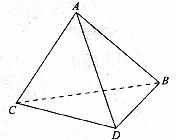
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直。若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(1)求证:平面ABD⊥平面ACD;
(2)求二面角A―CD―B的平面角的正切值;
(3)设过直线AD且与BC平行的平面为![]() ,求点B到平面
,求点B到平面![]() 的距离。
的距离。
科目:高中数学 来源: 题型:
 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省襄樊四中高二(上)数学测试卷9(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com