
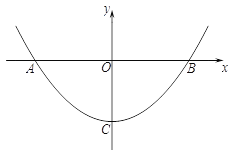
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,且位于x轴下方.
(1)如下图,若P(1,-3)、B(4,0),① 求该抛物线的解析式;② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
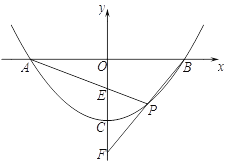
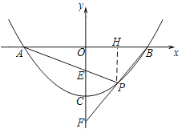
(2) 如下图,在图中的抛物线解析式不变的条件下,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,OE+OF是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】(1)①![]() ;②
;②![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)①根据待定系数法求函数解析式,可得答案;
②根据平行线的判定,可得![]() ,根据函数值相等两点关于对称轴对称,可得D点坐标;
,根据函数值相等两点关于对称轴对称,可得D点坐标;
(2)作![]() 于Q点,设
于Q点,设![]() ,可表示出
,可表示出![]() 的长,可得答案.
的长,可得答案.
(1)①将P(1,-3)、B(4,0)代入y=ax2+c得
![]() ,解得
,解得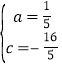 ,抛物线的解析式为:
,抛物线的解析式为:![]() .
.
②如图:
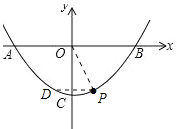
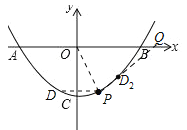
由∠DPO=∠POB得DP∥OB,D与P关于y轴对称,P(1,-3)得D(-1,-3);
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,∴Q(5,0),则直线PD2为![]() ,
,
再联立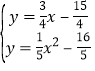 得:x=1或
得:x=1或![]() ,∴ D2(
,∴ D2(![]() )
)
∴点D的坐标为(-1,-3)或(![]() )
)
(2)过点P作PH⊥AB,设P(x,![]() )有OH=x,PH=
)有OH=x,PH=![]() ,
,
易证:△PAH∽△EAO,则 ![]() 即
即![]() ,∴
,∴![]() ,
,
同理得![]() ∴
∴![]() ,∴
,∴![]() ,则OE+OF=
,则OE+OF=![]()
∴OE+OF是定值,等于![]() 。
。


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线 ![]() (t为参数,t∈R),曲线
(t为参数,t∈R),曲线 ![]() (θ为参数,θ∈[0,2π]).
(θ为参数,θ∈[0,2π]).
(Ⅰ)以O为极点,x轴正半轴为极轴,取相同的长度单位建立极坐标系,求曲线C2的极坐标方程;
(Ⅱ)若曲线C1与曲线C2相交于点A、B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】输入x,求函数y=![]() 的值的程序框图如图C17所示.
的值的程序框图如图C17所示.
(1)指出程序框图中的错误之处并写出正确的算法步骤.
(2)重新绘制程序框图,并回答下面提出的问题.
①要使输出的值为7,则输入的x的值应为多少?
②要使输出的值为正数,则输入的x应满足什么条件?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为等比数列,
为等比数列,![]() ,公比为
,公比为![]() ,且
,且![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() ,求
,求![]() ;
;
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() ,使得对任意正整数
,使得对任意正整数![]() ,不等式
,不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,设动点
中,设动点![]() 到两定点
到两定点![]() ,
, ![]() 的距离的比值为
的距离的比值为![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若直线![]() 过点
过点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程,并判断直线
的方程,并判断直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,P为双曲线 ![]() ﹣y2=1(a>0)上一点,过P作两条渐近线的平行线交点分别为A,B,若平行四边形OAPB的面积为
﹣y2=1(a>0)上一点,过P作两条渐近线的平行线交点分别为A,B,若平行四边形OAPB的面积为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )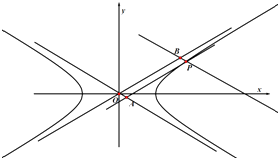
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2=
+y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2= ![]() 相切于点W(O为坐标原点).
相切于点W(O为坐标原点).
(1)证明:OE⊥OF;
(2)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的右准线方程为
的右准线方程为![]() ,又离心率为
,又离心率为![]() ,椭圆的左顶点为
,椭圆的左顶点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为椭圆上异于
为椭圆上异于![]() 任意一点.
任意一点.
(1)求椭圆的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com