
分析 (1)利用双曲线的离心率,以及虚轴长,求解a,b,得到双曲线的方程.
(2)利用双曲线的简单性质以及定义,结合余弦定理三角形的面积公式求解即可.
解答 解:(1)∵2b=2∴b=1
又$e=\frac{c}{a}$=$\frac{{\sqrt{5}}}{2}$∴${e^2}=\frac{c^2}{a^2}=\frac{{{a^2}+{b^2}}}{a^2}=1+\frac{b^2}{a^2}=\frac{5}{4}$,
∴a2=4,
∴双曲线的方程为$\frac{x^2}{4}-{y^2}=1$.
(2)由双曲线方程可知$2a=4,2c=2\sqrt{5}$,
∴${|{{F_1}{F_2}}|^2}=20$,
由双曲线定义有||PF1|-|PF2||=4
两边平方得${|{P{F_1}}|^2}+{|{P{F_2}}|^2}-2|{P{F_1}}||{P{F_2}}|=16$-------①
由余弦定理,有$|{F}_{1}{F}_{2}{|}^{2}=|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-2|P{F}_{1}||P{F}_{2}|cos6{0°}^{\;}$,
∴${|{P{F_1}}|^2}+{|{P{F_2}}|^2}-|{P{F_1}}||{P{F_2}}|=20$----------②
由①②可得|PF1||PF2|=20-16=4,
∴${S}_{△{F}_{1}P{F}_{2}}=\frac{1}{2}|P{F}_{1}||P{F}_{2}|sin6{0°}^{\;}=\frac{1}{2}×4×\frac{\sqrt{3}}{2}=\sqrt{3}$.
点评 本题考查直线与双曲线的位置关系的综合应用,双曲线的简单性质的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 为60.316kg | B. | 约为60.316kg | C. | 大于60.316kg | D. | 小于60.316kg |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
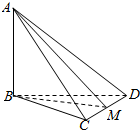
| A. | ∠ADB | B. | ∠BDC | C. | ∠AMB | D. | ∠ACB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com