
(12分)如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,

(1)求证:平面A B1D1∥平面EFG;
(2)求证:平面AA1C⊥面EFG.
(3)求异面直线AC与A1B所成的角
(1)先证平面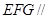 平面
平面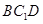 ,再证平面
,再证平面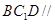 平面
平面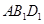 ,从而可证结论;
,从而可证结论;
(2)先证EF⊥AC,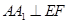 , 从而证明EF⊥平面
, 从而证明EF⊥平面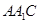 ,进而可证结论;
,进而可证结论;
(3)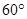
【解析】
试题分析:(1)∵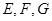 分别是
分别是 的中点,
的中点,
∴ ,
,
∴平面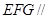 平面
平面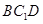 ,
,
又∵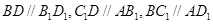 ,
,
∴平面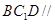 平面
平面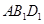 ,
,
∴平面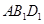 ∥平面
∥平面 . ……4分
. ……4分
(2)∵EF∥BD ,ABCD为正方形
∴BD⊥AC, 即EF⊥AC,
又∵正方体中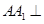 面ABCD,EF
面ABCD,EF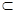 面ABCD, ∴
面ABCD, ∴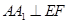 ,
,
∵ ,AC
,AC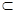 面
面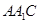 ,∴EF⊥平面
,∴EF⊥平面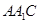 ,
,
又∵EF属于面EFG, ∴平面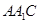 ⊥平面EFG. ……8分(3)在正方体中显然有
⊥平面EFG. ……8分(3)在正方体中显然有 ,
,
所以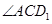 即为异面直线AC与A1B所成的角;
即为异面直线AC与A1B所成的角;
显然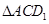 为正三角形,
为正三角形,
所以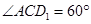 ,即异面直线AC与A1B所成的角为
,即异面直线AC与A1B所成的角为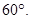 ……12分
……12分
考点:本小题主要考查面面平行、线面垂直的证明和线面角的求解。
点评:立体几何问题,主要考查学生的空间想象能力和推理论证能力,要紧扣相应的判定定理和性质定理,定理中要求的条件要一一列举出来,缺一不可.求角时,要先证后求,并注意角的取值范围.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| PO2 |
| 1 |
| PA2 |
| 1 |
| PB2 |
| 1 |
| PC2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com