
| A. | (0,$\frac{\sqrt{7}}{3}$] | B. | (0,$\frac{\sqrt{5}}{2}$] | C. | ($\sqrt{2}$,$\frac{5}{3}$] | D. | ($\sqrt{2}$,$\frac{\sqrt{13}}{3}$] |
分析 设G点的横坐标为x0,注意到x0≥a.由双曲线第二定义得:|GF1|=a+ex0,|GF2|=ex0-a,利用|GF1|-7|GF2|=0,可得a+ex0=7(ex0-a),x0=$\frac{4a}{3e}$≥a,由此即可得出结论.
解答 解:设G点的横坐标为x0,注意到x0≥a.
由双曲线第二定义得:|GF1|=a+ex0,|GF2|=ex0-a,
∵|GF1|-7|GF2|=0,
∴a+ex0=7(ex0-a),
∴x0=$\frac{4a}{3e}$≥a,
∴1<e≤$\frac{4}{3}$,
∴0<$\frac{b}{a}$≤$\frac{\sqrt{7}}{3}$,
∴C经过第一象限的渐近线的斜率的取值范围是(0,$\frac{\sqrt{7}}{3}$].
故选A.
点评 本题主要考查了双曲线的应用.考查了学生综合运用所学知识解决问题能力.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:填空题
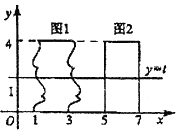 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
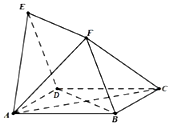 如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,平面四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com