
【题目】已知曲线C1的参数方程是![]() (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为![]() .
.
(1)求点A,B,C,D的直角坐标;
(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心, ![]() OA为半径作圆.
OA为半径作圆. 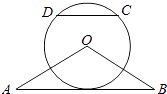
(1)证明:直线AB与⊙O相切;
(2)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M是满足下列条件的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)=Tf(x)成立.给出如下函数:①f(x)=x;②f(x)=2x;③f(x)= ![]() ;④f(x)=x2;则属于集合M的函数个数为( )
;④f(x)=x2;则属于集合M的函数个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且在区间(0,+∞)上是单调递增,若 ![]() ,△ABC的内角满足f(cosA)<0,则A的取值范围是( )
,△ABC的内角满足f(cosA)<0,则A的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,π)
,π)
C.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
D.( ![]() ,
, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的左焦点为F1有一小球A 从F1处以速度v开始沿直线运动,经椭圆壁反射(无论经过几次反射速度大小始终保持不变,小球半径忽略不计),若小球第一次回到F1时,它所用的最长时间是最短时间的5倍,则椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域,值域分别为A,B,且A∩B是单元集,下列命题中:
①若A∩B={a},则f(a)=a;
②若B不是单元集,则满足f[f(x)]=f(x)的x值可能不存在;
③若f(x)具有奇偶性,则f(x)可能为偶函数;
④若f(x)不是常数函数,则f(x)不可能为周期函数.
正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 ![]() 与p,且乙投球2次均未命中的概率为
与p,且乙投球2次均未命中的概率为 ![]() .
.
(1)求乙投球的命中率p;
(2)若甲投球1次,乙投球2次,两人共命中的次数记为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com