分析:(I)设数列{a
n}的首项为a
1,公差为d,解关于a
1与d的方程组,可求得a
1=2,d=4,从而可求a
n,继而可求b
n;
(Ⅱ)通过分组求和的方法可求得T
2n,然后将T
2n与2n
2+
作差,T
2n-(2n
2+
)=
(4
n-4n-1),验证n=1,2,3,时的符号,从而作出猜想,再用数学归纳法证明即可.
解答:解:(I)设数列{a
n}的首项为a
1,公差为d,
在S
2n-1=
an2中,令n=1,2,得
即
…2分
解得a
1=2,d=4,d=-2(舍去),
∴a
n=4n-2…4分
∴b
n=
…5分
(Ⅱ)T
2n=1+2×2-3+2
2+2×4-3+2
4+…+2
2n-2+2×2n-3…9分
=1+2
2+2
4+…+2
2n-2+4(1+2+…+n)-3n
=
+4•
-3n
=
-
+2n
2-n…8分
∴T
2n-(2n
2+
)=
(4
n-4n-1),
当n=1时,
(4
n-4n-1)=-
<0;
当n=2时,
(4
n-4n-1)=
>0;
当n=3时,
(4
n-4n-1)=
>0;
…
猜想当n≥2时,T
2n>2n
2+
,即n≥2时,4
n>4n+1.
下面用数学归纳法证明:
①当n=2时,4
2=16,4×2+1=9,16>9,成立;
②假设当n=k(k≥2)时成立,即4
k>4k+1.
则当n=k+1时,4
k+1=4•4
k>4(4k+1)=16k+4>4k+5=4(k+1)+1,
∴n=k+1时成立.
由①②得,当n≥2时,4
n>4n+1成立…11分
综上,当n=1时,T
2n<2n
2+
,
当n≥2时,T
2n>2n
2+
…12分
点评:本题考查数列递推式,考查数学归纳法的应用,考查化归思想、分类讨论思想、方程思想的综合应用,属于难题.



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案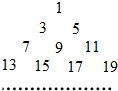 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足