【题目】某外卖企业两位员工今年
月某
天日派送外卖量的数据（单位：件），如茎叶图所示针对这天的数据，下面说法错误的是（ ）
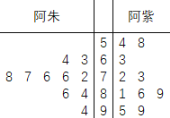
A.阿朱的日派送量的众数为
B.阿紫的日派送量的中位数为
C.阿朱的日派送量的中位数为D.阿朱的日派送外卖量更稳定
口算能手系列答案科目：高中数学 来源： 题型：
【题目】设
是一个
的方格表，在每一个小方格内各填一个正整数.若中的一个
方格表的所有数的和为10的倍数，则称其为“好矩形”；若中的一个
的小方格不包含于任何一个好矩形，则称其为“坏格”.求中坏格个数的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分，（1）小问7分，（2）小问5分）
设函数
（1）若
在
处取得极值，确定
的值，并求此时曲线
在点
处的切线方程；
（2）若在
上为减函数，求
的取值范围。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设等比数列｛
｝的公比为 q(q > 0，q = 1)，前 n 项和为 Sn，且 2a1a3 = a4，数列｛
｝的前 n 项和 Tn 满足2Tn = n(bn - 1)，n ∈N＊，b2 = 1.
(1) 求数列 ｛｝，｛｝的通项公式；
(2) 是否存在常数 t，使得 {Sn+ 
} 为等比数列？说明理由；
(3) 设 cn =
，对于任意给定的正整数 k(k ≥2), 是否存在正整数 l，m(k < l < m), 使得 ck，c1，cm 成等差数列？若存在，求出 l，m（用 k 表示），若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了各级城市的大街小巷，为了解我市的市民对共享单车的满意度，某调查机构借助网络进行了问卷调查，并从参与调查的网友中随机抽取了
人进行分析.若得分低于
分，说明不满意，若得分不低于分，说明满意，调查满意度得分情况结果用茎叶图表示如图1.
（Ⅰ）根据茎叶图完成下面列联表，并根据以上数据，判断是否有
的把握认为满意度与年龄有关；
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
（Ⅱ）先采用分层抽样的方法从
岁及以下的网友中选取
人，再从这人中随机选出
人，将频率视为概率，求选出的人中至少有
人是不满意的概率.
（Ⅲ）将频率视为概率，从参与调查的岁以上的网友中，随机选取
人，记其中满意度为满意的人数为
，求的分布列和数学期望.
参考格式：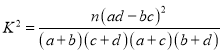
，其中
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，已知椭圆
的离心率为
，且右焦点到右准线
的距离为1．过
轴上一点
为常数，且
的直线与椭圆
交于
两点，与交于点
，
是弦
的中点，直线
与交于点
．
（1）求椭圆的标准方程；
（2）试判断以
为直径的圆是否经过定点？若是，求出定点坐标；若不是，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数学的对称美在中国传统文化中多有体现，譬如如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的和谐美.如果能够将圆的周长和面积同时平分的函数称为这个圆的“优美函数”，下列说法正确的是( )
A.对于任意一个圆，其“优美函数”有无数个
B.
可以是某个圆的“优美函数”
C.正弦函数
可以同时是无数个圆的“优美函数”
D.函数
是“优美函数”的充要条件为函数的图象是中心对称图形
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：对于任意
，
仍为数列
中的项，则称数列为“回归数列”．
（1）己知
()，判断数列
是否为“回归数列”，并说明理由；
（2）若数列
为“回归数列”，
，
，且对于任意，均有
成立．①求数列的通项公式；②求所有的正整数s，t，使得等式
成立．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
