
| A. | ①② | B. | ①③ | C. | ①②③ | D. | ①③④ |
分析 利用三角函数的周期性,和三角函数的图象和性质对选项逐个分析即可.
解答 解:①函数y=tanx中ω=1,故周期T=$\frac{π}{1}$=π;因为利用正切函数的图象可得在(0,$\frac{π}{2}$)上单调递增,所以A正确;
③y=sin|x|为偶函数,根据图象判断它不是周期函数,所以B不正确;
③由于函数y=|sinx|周期为$\frac{1}{2}$•2π=π,利用正弦函数的图象可得在(0,$\frac{π}{2}$)上单调递增,故正确;
④y=|cosx|是周期为π的三角函数,利用余弦函数的图象可得在(0,$\frac{π}{2}$)上单调递减,故不正确;
故选:B.
点评 本题考查三角函数的周期性及其求法,考查了三角函数的图象和性质,熟练掌握各类三角函数的周期情况及求法是解决问题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 计算1+3+5+…+2016 | |
| B. | 计算1×3×5×…×2016 | |
| C. | 求方程1×3×5×…×i=2016中的i值 | |
| D. | 求满足1×3×5×…×i>2016中的最小整数i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
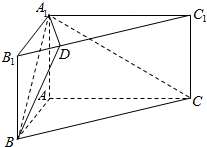 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
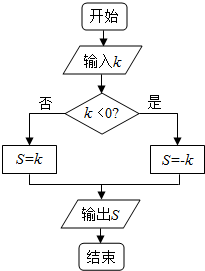 直线l的倾斜角为$\frac{π}{3}$,将l绕它与x轴的交点逆时针方向旋转$\frac{π}{2}$后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )
直线l的倾斜角为$\frac{π}{3}$,将l绕它与x轴的交点逆时针方向旋转$\frac{π}{2}$后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
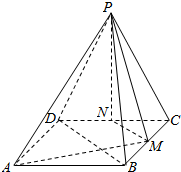 如图,在四棱锥P-ABCD中,侧面PCD丄底面ABCD,△PCD为等边三角形,M为BC中点,N为CD中点.若底面ABCD是矩形且AD=2$\sqrt{2}$,AB=2.
如图,在四棱锥P-ABCD中,侧面PCD丄底面ABCD,△PCD为等边三角形,M为BC中点,N为CD中点.若底面ABCD是矩形且AD=2$\sqrt{2}$,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com