
【题目】设M=10a2+81a+207,P=a+2,Q=26﹣2a,若将lgM,lgQ,lgP适当排序后可构成公差为1的等差数列{an}的前三项. (Ⅰ)求a的值及{an}的通项公式;
(Ⅱ)记函数 ![]() 的图像在x轴上截得的线段长为bn , 设
的图像在x轴上截得的线段长为bn , 设 ![]() ,求Tn .
,求Tn .
【答案】解:(Ⅰ)依题意有﹣2<a<13, ∵M﹣P=10a2+80a+205>0,M﹣Q=10a2+83a+181>0,
∴M最大.
又P﹣Q=﹣24+3a,
当﹣2<a<8时,P<Q,lgP+1=lgQ.
∴10P=Q,
∴ ![]() ,此时M>Q>P,且满足lgM=1+lgQ.
,此时M>Q>P,且满足lgM=1+lgQ.
∴ ![]() 符合题意.
符合题意.
当8<a<13时,P>Q,lgP=1+lgQ.
∴10Q=P,
∴ ![]() .
.
但此时不满足lgM=1+lgP.
∴ ![]() .
.
∴{an}的前三项为lgP,lgQ,lgM,此时 ![]() .
.
∴an=lgP+(n﹣1)×1=n﹣2lg2.
(Ⅱ)∵2an+1=an+an+2
∴x=﹣1是函数 ![]() 的零点
的零点
即f(x)=0时,(x+1)(anx+an+2)=0
∴ 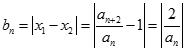 ,||bn=|x1﹣x2|=
,||bn=|x1﹣x2|= 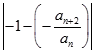
又∵an=n﹣2lg2>0,
∴ ![]() ,
,
∴ 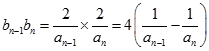 .
.
∴ 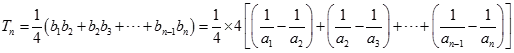
= ![]()
= ![]()
【解析】(Ⅰ)依题意有﹣2<a<13,利用作差法可比较M,P,Q中M最大,而P,Q的大小需要根据a的范围来确定,结合等差数列及对数的运算性质可求出满足题意的a及通项(Ⅱ)由等差数列的性质可得,2an+1=an+an+2 , 由f(x)=0时,(x+1)(anx+an+2)=0,从而可求得 ![]() ,结合an=n﹣2lg2>0,可得bn , 然后代入,利用裂项求和即可
,结合an=n﹣2lg2>0,可得bn , 然后代入,利用裂项求和即可
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系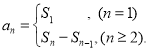 ),还要掌握等差数列的性质(在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列)的相关知识才是答题的关键.
),还要掌握等差数列的性质(在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,已知E为棱CC1上的动点. 
(1)求证:A1E⊥BD;
(2)是否存在这样的E点,使得平面A1BD⊥平面EBD?若存在,请找出这样的E点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解各校《国学》课程的教学效果,组织全市各学校高二年级全体学生参加了国学知识水平测试,测试成绩从高到低依次分为A、B、C、D四个等级.随机调阅了甲、乙两所学校各60名学生的成绩,得到如下的分布图: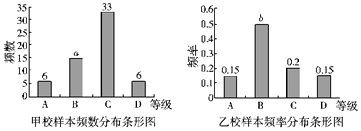
(Ⅰ)试确定图中 ![]() 与
与 ![]() 的值;
的值;
(Ⅱ)若将等级A、B、C、D依次按照 ![]() 分、80分、60分、50分转换成分数,试分别估计两校学生国学成绩的均值;
分、80分、60分、50分转换成分数,试分别估计两校学生国学成绩的均值;
(Ⅲ)从两校获得A等级的同学中按比例抽取5人参加集训,集训后由于成绩相当,决定从中随机选2人代表本市参加省级比赛,求两人来自同一学校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一高中经过层层上报,被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队,队员来自高中三个年级,人数为50人.视力对踢足球有一定的影响,因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间,将测量结果按如下方式分成6组:第一组[4.75,4.85),第二组[4.85,4.95),…,第6组[5.25,5.35],如图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中,全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布N(5.01,0.0064). 参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,
P(μ﹣2σ<ξ≤μ+2σ)=0.9544,P(μ﹣3σ<ξ≤μ+3σ)=0.9974.
(1)试评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况; 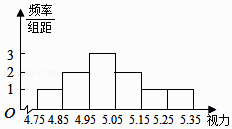
(2)求这50名队员视力在5.15以上(含5.15)的人数;
(3)在这50名队员视力在5.15以上(含5.15)的人中任意抽取2人,该2人中视力排名(从高到低)在全省喜爱足球的高中生中前130名的人数记为ξ,求ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为△ABC的外心,若 ![]() +
+ ![]() +
+ ![]() =
= ![]() ,则M是△ABC的( )
,则M是△ABC的( )
A.重心(三条中线交点)
B.内心(三条角平分线交点)
C.垂心(三条高线交点)
D.外心(三边中垂线交点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需用A,B两种原料,已知每种产品各生产1吨所需原料及每天原料的可用限额如下表所示,如果生产1吨甲产品可获利润3万元,生产1吨乙产品可获利4万元,则该企业每天可获得最大利润为万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABCD﹣A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1 , AB=3 ![]() ,∠BAD=60°,点E是△ABD的重心,且A1E=4.
,∠BAD=60°,点E是△ABD的重心,且A1E=4. 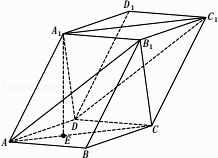
(1)求证:平面A1DC1∥平面AB1C;
(2)求二面角B1﹣AC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在(﹣∞,+∞)上的增函数,实数a使得f(1﹣ax﹣x2)<f(2﹣a)对于任意x∈[0,1]都成立,则实数a的取值范围是( )
A.(﹣∞,1)
B.[﹣2,0]
C.(﹣2﹣2 ![]() ,﹣2+2
,﹣2+2 ![]() )
)
D.[0,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=3,n(an+1﹣an)=an+1,n∈N*若对于任意的a∈[﹣1,1],n∈N* , 不等式 ![]() ﹣2at+1恒成立,则实数t的取值范围是 .
﹣2at+1恒成立,则实数t的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com