Question

某校高一年级共有320人，为调查高一年级学生每天晚自习自主支配学习时间（指除了完成老师布置的作业后学生根据自己的需要进行学习的时间）情况，学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查．根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据（单位：分钟），按照以下区间分为七组：①[0，10），②[10，20），③[20，30），④[30，40），⑤[40，50），⑥[50，60），⑦[60，70），得到频率分布直方图如图．已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人．

（1）求n的值；

（2）若高一全体学生平均每天晚自习自主支配学习时间少于45分钟，则学校需要减少作业量．根据以上抽样调查数据，学校是否需要减少作业量？

（注：统计方法中，同一组数据常用该组区间的中点值作为代表）

（3）问卷调查完成后，学校从第3组和第4组学生中利用分层抽样的方法抽取7名学生进行座谈，了解各学科的作业布置情况，并从这7人中随机抽取两名学生聘为学情调查联系人。求第3组中至少有1名学生被聘为学情调查联系人的概率。

 

 

 

Answer 1

【答案】

（1）由图知第1组和第2组的频率分别是0.02和0.06，

则n×（0.02+0.06）=4，解得n=50

（2）设第i组的频率和频数分别是pi和xi，由图知p1=0.02，p2=0.06，p3=0.3，p4=0.4，p5=0.12，p6=0.08，p7=0.02，则由xi=50×pi，

可得x1=1，x2=3，x3=15，x4=20，x5=6，x6=6，x7=1

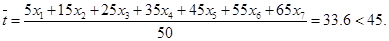
则高一学生每天平均自主支配时间是则学校需要减少作业量

（3）第3组和第4组的频数分别是15和20，用分层抽样的方法抽取7人，则第3组应抽（人），第4组应抽（人）。

设第3组中被抽到的3名学生分别是甲、乙、丙，第4组被抽到的4名学生分别是a、b、c、d，则从7人中抽取2人的基本事件空间Ω＝{（甲，乙），（甲，丙），（甲，a），（甲，b），（甲，c），（甲，d），（乙，丙），（乙，a），（乙，b），（乙，c），（乙，d）（丙，a）（丙，b），（丙，c），（丙，d），（a，b），（a，c），（a，d），（b，c），（b，d），（c，d）}，共21个基本事件。

设事件A为“第3组中至少有1名学生被选聘”，则事件A共有15个基本事件，则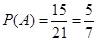，即第3组中至少有1名学生被选聘的概率是。

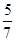【解析】略