
【题目】一个盒子中装有1个黑球和2个白球,这3个球除颜色外完全相同.有放回地连续抽取2次,每次从中任意地取出1个球.计算下列事件的概率:
(1)取出的两个球都是白球;
(2)第一次取出白球,第二取出黑球;
(3)取出的两个球中至少有一个白球.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)写出所有的基本事件,得出基本事件总数,统计出取出的两个球都是白球所包含的基本事件个数,即可得到概率;
(2)统计出第一次取出白球,第二次取出黑球包含的基本事件个数即可得解;
(3)求出其对立事件“取出的两个全是黑球”的概率,即可求解.
(1)把2个白球记为白1,白2.
所有样本点:(黑,黑),(黑,白1),(黑,白2),(白1,黑),(白1,白1),(白1,白2),(白2,黑),(白2,白1),(白2,白2),共9个.
设“取出的两个球都是白球”为事件![]() ,则事件
,则事件![]() 包含的样本点有(白1,白1),(白1,白2),(白2,白1),(白2,白2),共4个.
包含的样本点有(白1,白1),(白1,白2),(白2,白1),(白2,白2),共4个.
故取出的两个球都是白球的概率![]() .
.
(2)设“第一次取出白球,第二次取出黑球”为事件![]() ,则事件
,则事件![]() 包含的样本点有(白1,黑),(白2,黑),共2个.
包含的样本点有(白1,黑),(白2,黑),共2个.
故第一次取出白球,第二次取出黑球的概率![]() .
.
(3)设“取出的两个球中至少有一个白球”为事件![]() ,
,
则![]() 表示“取出的两个球都是黑球”,
表示“取出的两个球都是黑球”,![]() 包含的样本点只有1个,则
包含的样本点只有1个,则![]() 包含的样本点有8个,
包含的样本点有8个,
故取出的两个球中至少有一个白球的概率![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2018年8月教育部、国家卫生健康委员会等八个部门联合印发《综合防控儿童青少年近视实话方案》中明确要求,为切实加强新时代儿童青少年近视防控工作,学校应严格组织全体学生每天上、下午各大做1次眼保健操.为了了解学校推广眼保健操是否能有效预防近视,随机从甲学校抽取了50名学生,再从乙学校选出与甲学校被抽取的50名学生视力情况一样的50学生(期中甲学校每天安排学生做眼保健操,乙学校不安排做跟保健操),一段时间后检测他们的视力情况并统计,若视力情况为1.0及以上,则认为该学生视力良好,否则认为该学生的视力一般,表1为甲学校视力情况的频率分布表,表2为乙学校学生视力情况的频率分布表,根据表格回答下列问题:
表1 甲学校学生视力情况的频率分布表
视力情况 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
频 数 | 1 | 1 | 15 | 15 | 18 |
表2 乙学校学生视力情况的频率分布表
视力情况 | 0.5 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
频 数 | 2 | 2 | 4 | 19 | 13 | 10 |
(1)求在甲学校的50名学生中随机选择1名同学,求其视力情况为良好的概率;
(2)根据表1,表2,对在学校推广眼保健操的必要性进行分析;
(3)在乙学校视力情况一般的学生中选择2人,了解其具体用眼习惯,求这两人视力情况都为0.8的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的展开式中各项系数的和为2,则下列结论正确的有( )
的展开式中各项系数的和为2,则下列结论正确的有( )
A.![]()
B.展开式中常数项为160
C.展开式系数的绝对值的和1458
D.若![]() 为偶数,则展开式中
为偶数,则展开式中![]() 和
和![]() 的系数相等
的系数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
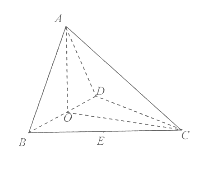
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,![]() ,
,![]() .
.
(1)求证:![]() 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的余弦值;
(3)求点E到平面ACD的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了 40 名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
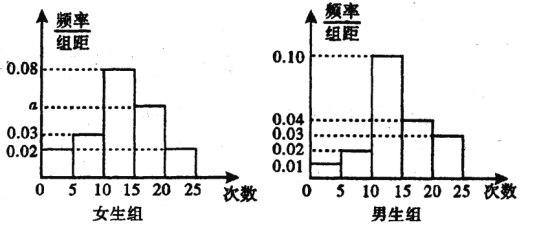
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
(1)求![]() 的值;
的值;
(2)求抽取的40名学生中月上网次数不少于15次的人数;
(3)再从月上网次数不少于20 次的学生中随机抽取2人,求至少抽到1名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
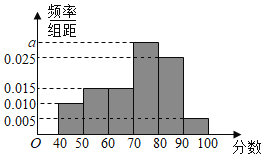
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
分组 | 频数 | 频率 | |
一组 | 0≤t<5 | 0 | 0 |
二组 | 5≤t<10 | 10 | 0.10 |
三组 | 10≤t<15 | 10 | ② |
四组 | 15≤t<20 | ① | 0.50 |
五组 | 20≤t≤25 | 30 | 0.30 |
合计 | 100 | 1.00 |

解答下列问题:
(1)这次抽样的样本容量是多少?
(2)在表中填写出缺失的数据并补全频率分布直方图;
(3)旅客购票用时的平均数可能落在哪一组?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com