
【题目】某辆汽车以x km/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为![]() ,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
(1)求k的值;
(2)求该汽车每小时油耗的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知定点A(0,1),B(0,﹣1),C(1,0),动点P满足: ![]() ,
,
(1)求动点P的轨迹方程,并说明方程表示的曲线类型;
(2)当k=2,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①向量 ![]() 与
与 ![]() 是共线向量,则A、B、C、D必在同一直线上;
是共线向量,则A、B、C、D必在同一直线上;
②向量 ![]() 与向量
与向量 ![]() 平行,则
平行,则 ![]() 方向相同或相反;
方向相同或相反;
③若下列向量 ![]() 、
、 ![]() 满足
满足 ![]() ,且
,且 ![]() 与
与 ![]() 同向,则
同向,则 ![]() ;
;
④若 ![]() ,则
,则 ![]() 的长度相等且方向相同或相反;
的长度相等且方向相同或相反;
⑤由于零向量方向不确定,故不能与任何向量平行.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的方格纸由若干个边长为1的小正方形并在一起组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且 ![]()
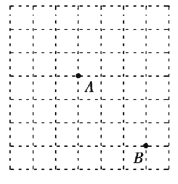
(1)画出所有的向量 ![]() ;
;
(2)求| ![]() |的最大值与最小值.
|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直角坐标系中曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, ![]() 点的极坐标
点的极坐标![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]()
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数,﹣π<α<0),曲线C2的参数方程为
(α为参数,﹣π<α<0),曲线C2的参数方程为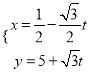 (t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1的极坐标方程和曲线C2的普通方程;
(2射线θ=﹣![]() 与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com