
【题目】已知存在常数![]() ,那么函数
,那么函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,再由函数的奇偶性可知在
上是增函数,再由函数的奇偶性可知在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(1)判断函数![]() 的单调性,并证明:
的单调性,并证明:
(2)将前述的函数![]() 和
和![]() 推广为更为一般形式的函数
推广为更为一般形式的函数![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的单调性(只须归纳出结论,不必推理证明)
的单调性(只须归纳出结论,不必推理证明)
【答案】![]() 见解析;
见解析;![]() 见解析.
见解析.
【解析】
![]() 采用换元的思想:令
采用换元的思想:令![]() 则
则![]() ;再借助复合函数单调性的判断规则和奇偶函数在对称区间上的单调性特点,即可得证.
;再借助复合函数单调性的判断规则和奇偶函数在对称区间上的单调性特点,即可得证.
![]() 由
由![]() 结论和题中
结论和题中![]() 的性质进行归纳总结,即可得出一般性结论.
的性质进行归纳总结,即可得出一般性结论.
![]() 判断如下:
判断如下:
![]() 在
在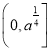 上为减函数,
上为减函数,
在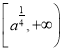 上为增函数;
上为增函数;
再由函数的奇偶性可知,
在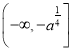 上为减函数,
上为减函数,
在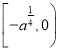 上为增函数.
上为增函数.
证明:令![]() ,
,
则![]() ,
,
由题可得,
![]() 在
在![]() 上为减函数,
上为减函数,
在![]() 上是增函数;
上是增函数;
![]() 在
在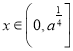 上为增函数,
上为增函数,
在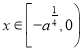 上为减函数;
上为减函数;
![]() 由复合函数单调性判断规则知:
由复合函数单调性判断规则知:
![]() 在
在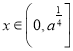 上为减函数,
上为减函数,
在 上为增函数;
上为增函数;
由题知,
![]() 为偶函数,
为偶函数,
![]() 偶函数在对称区间上单调性相反,
偶函数在对称区间上单调性相反,
![]()
![]() 在
在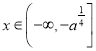 上为减函数,
上为减函数,
在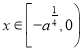 上为增函数;
上为增函数;
![]() 一般性结论:
一般性结论:
函数![]()
![]() 在
在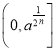 上为减函数,
上为减函数,
在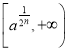 上为增函数;
上为增函数;
再由函数的奇偶性可知,
当n为奇数时,
在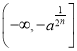 上为增函数,
上为增函数,
在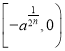 上为减函数;
上为减函数;
当n为偶数时,
在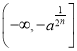 上为减函数,
上为减函数,
在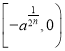 上为增函数;
上为增函数;


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】把三盆不同的兰花和4盆不同的玫瑰花摆放在右图图案中的1,2,3,4,5,6,7所示的位置上,其中三盆兰花不能放在一条直线上,则不同的摆放方法为( ) 
A.2680种
B.4320种
C.4920种
D.5140种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数F(a,b)= ![]() (a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
(a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
A.4
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABO﹣A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1 , OB=3,O1B1=1,OO1= ![]() .
. 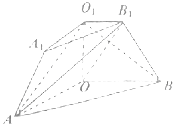
(1)证明:AB1⊥BO1;
(2)求直线AO1与平面AOB1所成的角的正切值;
(3)求二面角O﹣AB1﹣O1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别
的左右焦点分别![]()
![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆于
交椭圆于![]() 两点,满足
两点,满足![]() .
.
(1)求椭圆![]() 的离心率.
的离心率.
(2)![]() 是椭圆
是椭圆![]() 短轴的两个端点,设点
短轴的两个端点,设点![]() 是椭圆
是椭圆![]() 上一点(异于椭圆
上一点(异于椭圆![]() 的顶点),直线
的顶点),直线![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com