




科目:高中数学 来源: 题型:
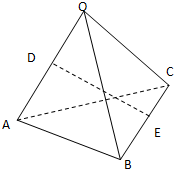 如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE
如图,空间四边形OABC各边以及AC,BO的边长都为a,点D,E分别是边OA,BC的中点,连接DE 查看答案和解析>>
科目:高中数学 来源:河南省汤阴一中2008届高三迎第一次市统考模拟数学试题(理) 题型:022
如图,在空间直角坐标系中平面的方程是x+2y+z-2=0,类比点到直线的距离公式,则点P(4,0,4)到平面ABC的距离是________.

查看答案和解析>>
科目:高中数学 来源: 题型:022
(2007
安徽江南十校模拟)如图所示,正方体ABCD—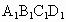 的棱长为1,E是
的棱长为1,E是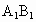 的中点,则下列五个命题:
的中点,则下列五个命题:
A.点E到平面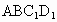 的距离是
的距离是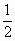 ;
;
B.直线BC与平面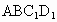 所成的角等于45°;
所成的角等于45°;
C.空间四边形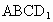 在正方体六个面内的射影围成的图形中,面积最小值为
在正方体六个面内的射影围成的图形中,面积最小值为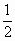 ;
;
D.BE
与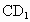 所成的角为
所成的角为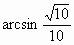 ;
;
E.二面角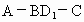 的大小为
的大小为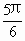
其中真命题是
________(按照原顺序写出所有真命题的代号).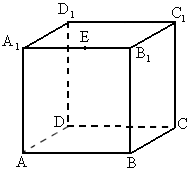
查看答案和解析>>
科目:高中数学 来源:2014届宁夏高二上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, .
. 于点
于点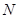 ,
,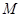 是
是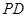 中点.
中点.
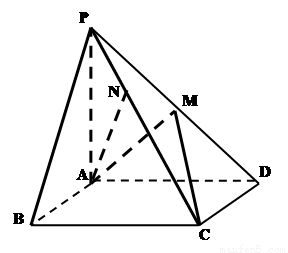
(1)用空间向量证明:AM⊥MC,平面 ⊥平面
⊥平面 ;
;
(2)求直线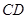 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(3)求点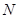 到平面
到平面 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)点B到平面α的距离;
(2)异面直线l与AB所成的角(用反三角函数表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com