练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】将一张边长为12cm的正方形纸片按如图（1）所示阴影部分裁去四个全等的等腰三角形，将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型，如图（2）所示放置．如果正四棱锥的主视图是等边三角形，如图（3）所示，则正四棱锥的体积是（ ）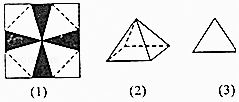
    A. cm3
    B. cm3
    C. cm3
    D. cm3

    【答案】B
    【解析】解：由题意可得：设裁去四个全等的等腰三角形的底边边长为x，则图（2）中的底面正方形的边长= ，又图（3）中的等边三角形的边长= ﹣ = ．

    ∴ （12﹣x）= ．

    解得x=4．

    ∴正四棱锥的体积= × = ．

    故选：B．

    【考点精析】本题主要考查了由三视图求面积、体积的相关知识点，需要掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的三个内角A、B、C所对的边长分别是a、b、c，且 ，若将函数f（x）=2sin（2x+B）的图象向右平移 个单位长度，得到函数g（x）的图象，则g（x）的解析式为（ ）
    A.
    B.
    C.2sin2x
    D.2cos2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将集合M={1，2，3，…15}表示为它的5个三元子集（三元集：含三个元素的集合）的并集，并且这些三元子集的元素之和都相等，则每个三元集的元素之和为；请写出满足上述条件的集合M的5个三元子集 ． （只写出一组）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为研究学生语言学科的学习情况，现对高二200名学生英语和语文某次考试成绩进行抽样分析．将200名学生编号为001，002，…，200，采用系统抽样的方法等距抽取10名学生，将10名学生的两科成绩（单位：分）绘成折线图如下：
    （Ⅰ）若第一段抽取的学生编号是006，写出第五段抽取的学生编号；
    （Ⅱ）在这两科成绩差超过20分的学生中随机抽取2人进行访谈，求2人成绩均是语文成绩高于英语成绩的概率；
    （Ⅲ）根据折线图，比较该校高二年级学生的语文和英语两科成绩，写出你的结论和理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣1+aex ．
    （1）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求a的值；
    （2）求f（x）的极值；
    （3）当a=1时，曲线y=f（x）与直线y=kx﹣1没有公共点，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正△ABC三个顶点都在半径为2的球面上，球心O到平面ABC的距离为1，点E是线段AB的中点，过点E作球O的截面，则截面面积的最小值是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义一个集合A的所有子集组成的集合叫做集合A的幂集，记为P(A)，用n(A)表示有限集A的元素个数，给出下列命题：①对于任意集合A，都有AP(A)；②存在集合A，使得n[P(A)]=3；③用表示空集，若A∩B=，则P(A)∩P(B)=；④若A B,，则P(A) P(B)；⑤若n(A)-n(B)=1，则n[P(A)]=2×n[P(B)]其中正确的命题个数为（ ）。
    A.4
    B.3
    C.2
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC是等边三角形，边长为4，BC边的中点为D，椭圆W以A，D为左、右两焦点，且经过B、C两点．
    （1）求该椭圆的标准方程；
    （2）过点D且x轴不垂直的直线l交椭圆于M，N两点，求证：直线BM与CN的交点在一条定直线上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的函数y=f（x），恒有f（x）=f（2﹣x）成立，且f′（x）（x﹣1）＞0，对任意的x1＜x2 ， 则f（x1）＜f（x2）成立的充要条件是（ ）
    A.x2＞x1≥1
    B.x1+x2＞2
    C.x1+x2≤2
    D.x2

    查看答案和解析>>

    同步练习册答案