
分析 (1)设出二次函数的一般形式后,代入f(0)=0且f(x+1)=f(x)+x+1,化简后根据多项式相等的条件求出a,b及c的值,即可确定出f(x)的解析式;
(2)确定g(x),即可求出f(g(x))的表达式.
解答 解:(1)令f(x)=ax2+bx+c(a≠0)
∵f(0)=0,
∴c=0,
∴f(x)=ax2+bx
∵f(x+1)=f(x)+x+1,
∴a(x+1)2+b(x+1)-(ax2+bx)=x+1,
∴2ax+a+b=x+1,即2a=1,a+b=1,
∴a=$\frac{1}{2}$,b=$\frac{1}{2}$,
∴f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x;
(2)g(x)=2f(-x)+x=2($\frac{1}{2}$x2-$\frac{1}{2}$x)+x=x2,
∴f(g(x))=$\frac{1}{2}$x4+$\frac{1}{2}$x2.
点评 此题考查学生会利用待定系数法求函数的解析式,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-2 | B. | a<-2 | C. | a>-2 | D. | a≥-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(理)试卷(解析版) 题型:选择题
设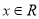 ,则“
,则“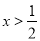 ”是“
”是“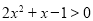 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com