
【题目】“微信运动”是一个类似计步数据库的公众帐号,用户只需以运动手环或手机协处理器的运动教据为介,然后关注该公众号,就能看见自己与好友每日行走的步数,并在同一排行榜上得以体现,现随机选取朋友圈中的50人记录了他们某一天的走路步数,并将数据整理如下:

规定:人一天行走的步数超过8000步时被系统评定为“积极性”,否则为“懈怠性”.
(1)填写下面列联表(单位:人),并根据列联表判断是否有![]() 的把握认为“评定类型与性别有关”;
的把握认为“评定类型与性别有关”;

附:
|
|
|
|
|
|
|
|
|
|
|
|

(2)为了进一步了解“懈怠性”人群中每个人的生活习惯,从步行在![]() 的人群中再随机抽取3人,求选中的人中男性人数超过女性人数的概率.
的人群中再随机抽取3人,求选中的人中男性人数超过女性人数的概率.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】黑板上写有,1,2,…,666,这666个正整数,第一步划去最前面的八个数:1,2,…,8,,并在666后面写上1,2,…,8的和36;第二步再划去最前面的八个数:9,10,…,16,并在最后面写上9,10,…,16的和100;如此继续下去(即每一步划去最前面的八个数,并在最后写上划去的八个数的和).
(1)问:经过多少步后,黑板上只剩下一个数?
(2)当黑板上只剩下一个数时,求出在黑板上出现过的所有数的和(如果一个数多次出现需重复计算).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高为4 m.养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(不含底面积);
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题
![]() 已知P为椭圆
已知P为椭圆![]() 上任意一点,
上任意一点,![]() ,
,![]() 是椭圆的两个焦点,则
是椭圆的两个焦点,则![]() 的范围是
的范围是![]() ;
;
![]() 已知M是双曲线
已知M是双曲线![]() 上任意一点,
上任意一点,![]() 是双曲线的右焦点,则
是双曲线的右焦点,则![]() ;
;
![]() 已知直线l过抛物线C:
已知直线l过抛物线C:![]() 的焦点F,且l与C交于
的焦点F,且l与C交于![]() ,
,![]() 两点,则
两点,则![]() ;
;
![]() 椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点
椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点![]() ,
,![]() 是它的焦点,长轴长为2a,焦距为2c,若静放在点
是它的焦点,长轴长为2a,焦距为2c,若静放在点![]() 的小球
的小球![]() 小球的半径忽略不计
小球的半径忽略不计![]() 从点
从点![]() 沿直线出发则经椭圆壁反射后第一次回到点
沿直线出发则经椭圆壁反射后第一次回到点![]() 时,小球经过的路程恰好是4a.
时,小球经过的路程恰好是4a.
其中正确命题的序号为______![]() 请将所有正确命题的序号都填上
请将所有正确命题的序号都填上![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月18日至10月24日,中国共产党第十九次全国代表大会![]() 简称党的“十九大”
简称党的“十九大”![]() 在北京召开
在北京召开![]() 一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在
一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在![]() 内,按成绩分成5组:第1组
内,按成绩分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
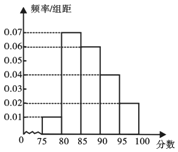
![]() 求这100人的平均得分
求这100人的平均得分![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 求第3,4,5组分别选取的作深入学习的人数;
求第3,4,5组分别选取的作深入学习的人数;
![]() 若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:点
为直径的圆经过坐标原点,证明:点![]() 到直线
到直线![]() 的距离为定值;
的距离为定值;
(III)在(Ⅱ)的条件下,试求![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com