考点:对数函数的图像与性质,对数的运算性质,根的存在性及根的个数判断
专题:导数的综合应用
分析:(1)求函数f(x)的定义域(-∞,0),再求导f′(x),从而讨论函数的单调性;
(2)讨论a的取值,从而利用函数的单调性及函数零点的判定定理求解零点的个数.
解答:
解:(1)∵函数f(x)=(2a
2+1)ln(-x)+a(2x-1),
∴-x>0,即x<0,
∴f(x)的定义域为(-∞,0);
对f(x)求导,得f′(x)=
•(-1)+2a=
+2a,
①当a≤0时,f′(x)<0,∴f(x)在(-∞,0)上是减函数;
②当a>0时,f′(x)=
+2a=
,
∴当x∈(-∞,-
)时,f′(x)>0,
x∈(-
,0)时,f′(x)<0,
∴f(x)在(-∞,-
)上是单调增函数,在(-
,0)上单调减函数;
(2)①当a=0时,f(x)=ln(-x),
令ln(-x)=0,解得x=-1,
∴f(x)在[-1,-
]上有一个零点;
②当a>0时,
∵
-1=
>0,
∴[-1,-
]⊆(-
,0),
即f(x)在[-1,-
]上是单调减函数,
又∵f(-1)=-3a<0,
f(-
)=-2a-(2a
2+1)ln2<0,
∴f(x)在[-1,-
]上没有零点;
③当a<0时,f(x)在[-1,-
]上单调递减,
又∵f(-1)=-3a>0,
f(-
)=-2a-(2a
2+1)ln2<0,
∴f(x)在[-1,-
]上有一个零点;
综上,a≤0时,f(x)在[-1,-
]有一个零点,
a>0时,f(x)在[-1,-
]上无零点.
点评:本题考查了求函数的定义域以及利用导数判断函数的单调性与零点的应用问题,是综合性题目.



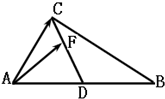 如图所示,在△ABC中,D为AB的中点,F在线段CD上,设
如图所示,在△ABC中,D为AB的中点,F在线段CD上,设