
【题目】已知函数 ![]() ,
,
(Ⅰ)证明: ![]() 为奇函数;
为奇函数;
(Ⅱ)判断 ![]() 单调性并证明;
单调性并证明;
(III)不等式 ![]() 对于
对于 ![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
【答案】解:(1)由 ![]() ,可证得函数为奇函数;(2)该函数为反比例型函数,利用单调性定义可证得函数在
,可证得函数为奇函数;(2)该函数为反比例型函数,利用单调性定义可证得函数在 ![]() 上为增函数。(3)利用函数的奇偶性和单调性,不等式可转化为
上为增函数。(3)利用函数的奇偶性和单调性,不等式可转化为 ![]() 恒成立,可求得
恒成立,可求得 ![]() 的取值范围。
的取值范围。
(Ⅰ) ![]() ,
, ![]() 为奇函数.
为奇函数.
(II) ![]() 在R上为增函数.
在R上为增函数.
![]() ,
,
在R内任取 ![]() ,
,
则 ![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() .
.
![]() 在R上为增函数.
在R上为增函数.
(III) ![]() ,
,
又 ![]() 在R上为增函数,
在R上为增函数,
![]() 恒成立,
恒成立, ![]() ,
,
即 ![]() 时,
时, ![]() ,
,
![]() ,解得
,解得 ![]() .
.
【解析】【分析(1)根据函数的奇偶性可知 f ( x ) = f ( x ) ,得出函数为奇函数。(2)根据函数的单调性的定义即可得证。(3)结合函数的奇偶性和单调性可得 x t ≥ t2 x 2 恒成立, x ∈ [ 1 , 2 ] ,整理上式借助二次函数在指定区间上的最值得到 ( x2 + x ) nim ≥ t 2 + t 即为t2 + t ≤ 2 解出即可。


科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 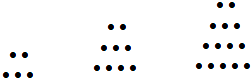
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准03.5,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.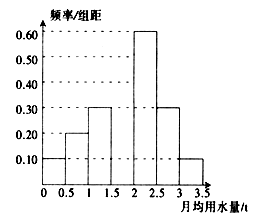
(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;
(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准03.5,则月均用水量的最低标准定为多少吨,请说明理由;
(3)从频率分布直方图中估计该100位居民月均用水量的平均数(同一组中的数据用该区间的中点值代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0 , y0),且y0<x0+2,则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣ ![]() ,0)
,0)
B.(﹣ ![]() ,0)
,0)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣∞,﹣ ![]() )∪(0,+∞)
)∪(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax﹣1(e为自然对数的底数). (Ⅰ)当a=1时,求过点(1,f(1))处的切线与坐标轴围成的三角形的面积;
(Ⅱ)若f(x)≥x2在(0,1)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= ![]() PD. (Ⅰ)证明:平面PQC⊥平面DCQ
PD. (Ⅰ)证明:平面PQC⊥平面DCQ
(Ⅱ)求二面角Q﹣BP﹣C的余弦值.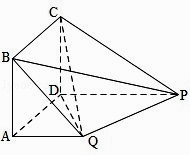
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=mx2+4x+1,且满足f(﹣1)=f(3).
(1)求函数f(x)的解析式;
(2)若函数f(x)的定义域为(﹣2,2),求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,cosx=2;命题q:x∈R,x2﹣x+1>0,则下列结论中正确的是( )
A.p∨q是假命题
B.p∧q是真命题
C.(¬p)∧(¬q)是真命题
D.(¬p)∨(¬q)是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com