
����Ŀ���ź����һ�������˷dz�ϲ�����ֻ�Ӧ��.ij������Ӫ�̶Լס�������Ʒ�Ƹ�![]() ���ͺŵ��ֻ�����ͬ��������������ĸ�������ͳ�ƣ��õ��������ݣ�
���ͺŵ��ֻ�����ͬ��������������ĸ�������ͳ�ƣ��õ��������ݣ�
Ʒ�� �ͺ� | �� | �� | �� | �� | �� |
��Ʒ�ƣ����� | 4 | 3 | 8 | 6 | 12 |
��Ʒ�ƣ����� | 5 | 7 | 9 | 4 | 3 |
������� �ֻ�Ʒ�� | ���� | һ�� | �ϼ� |
��Ʒ�ƣ����� | |||
��Ʒ�ƣ����� | |||
�ϼ� |
����������������������![]() �����ֻ��ͺ�Ϊ��������������Ϊ��һ�㡱����������������ݴ��ж��Ƿ���
�����ֻ��ͺ�Ϊ��������������Ϊ��һ�㡱����������������ݴ��ж��Ƿ���![]() �İ�����Ϊ��������ĸ������ֻ�Ʒ���йأ�
�İ�����Ϊ��������ĸ������ֻ�Ʒ���йأ�
���������������أ���Ҫ�Ӽס�����Ʒ�Ƶ�![]() ���ͺ��и�ѡ��
���ͺ��и�ѡ��![]() ���ͺŵ��ֻ����д��������ǡ��һ���ͺ��ǡ�����������һ���ͺ��ǡ�һ�㡱�ĸ��ʣ�
���ͺŵ��ֻ����д��������ǡ��һ���ͺ��ǡ�����������һ���ͺ��ǡ�һ�㡱�ĸ��ʣ�
�ο���ʽ���������![]() �Ĺ۲�ֵ���㹫ʽ��
�Ĺ۲�ֵ���㹫ʽ��![]() ��
��
����![]() .�ٽ�ֵ����
.�ٽ�ֵ����
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
���𰸡�(1)�����������û��90%�İ�����Ϊ��������ĸ������ֻ�Ʒ���йأ�
(2) ![]() .
.
����������������I�����ݱ�����������![]() �б����������ٽ�ֵ�Ĺ�ʽ������۲�ֵ�����ù۲�ֵͬ�ٽ�ֵ�������ж���
�б����������ٽ�ֵ�Ĺ�ʽ������۲�ֵ�����ù۲�ֵͬ�ٽ�ֵ�������ж���
�����ǡ���ѡ�������ͺ��У�һ���ͺ��ǡ�����������һ���ͺ��ǡ�һ�㡱��Ϊ�¼�A���������ͺ��У���ѡһ�֡�����5��5=25�ַ����������ͺ��У�һ���ͺ��ǡ�����������һ���ͺ��ǡ�һ�㡱��Ϊ����������ֱ�����ж����֣������������.
�������I��
![]() ��
��
���ԣ�û��90%�İ�����Ϊ��������ĸ������ֻ�Ʒ���йأ�
�����ǡ���ѡ�������ͺ��У�һ���ͺ��ǡ�����������һ���ͺ��ǡ�һ�㡱��Ϊ�¼�A��
�������еı������ݿɵã�
�������ͺ��У���ѡһ�֡�����5��5=25�ַ�����
���ͺš������������ͺš�һ�㡱����3��3=9�ַ�����
���ͺš�һ�㡱�����ͺš�����������2��2=4�ַ�����
���ԣ�![]() ��
��


 Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x+m|��
���� �����m�IJ���ʽf��1��+f����2����5��
����x��0ʱ��֤���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�е���ȫ�߹����ĸ���վ���ס�������ͬʱ�ڵ�����1�ų�վ����վ���˳�������ÿ���Ե�2��վ��ʼ����ÿ����վ�³��ǵȿ��ܵģ�Լ��������ʵ����![]() ��ʾ������
��ʾ������![]() �ų�վ�³�������
�ų�վ�³�������![]() �ų�վ�³���
�ų�վ�³���
������������ʵ���Ѽס��������³������п��ܵĽ���оٳ�����
��������ס�������ͬ�ڵ�3�ų�վ�³��ĸ��ʣ�
��������ס��������ڲ�ͬ�ij�վ�³��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ200��ѧ������ѧ���п��Գɼ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ�����������![]() .
.
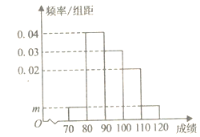
��1����ͼ��m��ֵ��
��2������Ƶ�ʷֲ�ֱ��ͼ��������200��ѧ����ƽ���֣�ͬһ���е������ø���������м�ֵ������������λ������������ȡ��������
��3������200��ѧ������ѧ�ɼ��У�ijЩ�����ε�����x��Ӣ��ɼ���Ӧ�����ε�����y֮�����±���ʾ����Ӣ��ɼ���![]() ������.
������.
������ | [70��80�� | [80��90�� | [90��100�� | [100��110�� | [110��120�� |
x��y | 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ���²�Ʒ�ij���(��λ��![]() )���м�⣬����ͼ�Ǽ������Ƶ�ʷֲ�ֱ��ͼ���ݴ˹���������Ʒ����λ����ƽ�����ֱ�Ϊ( )
)���м�⣬����ͼ�Ǽ������Ƶ�ʷֲ�ֱ��ͼ���ݴ˹���������Ʒ����λ����ƽ�����ֱ�Ϊ( )

A.20��22.5B.22.5��25C.22.5��22.75D.22.75��22.75
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����գ�x��= ![]() ��a��0
��a��0
��1��������f��x��=lnx+�գ�x�����ڣ�1��2����ֻ��һ����ֵ�㣬��a��ȡֵ��Χ��
��2����g��x��=|lnx|+�գ�x�����Ҷ�����x1 �� x2�ʣ�0��2]����x1��x2 �� ���� ![]() ����1����a��ȡֵ��Χ��
����1����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ���ҹ���
���ҹ���![]() .
.
��������Բ![]() �ķ��̣�
�ķ��̣�
������![]() Ϊ��Բ
Ϊ��Բ![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() .ȡ��
.ȡ��![]() ������
������![]() ������
������![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ���ڵ�
���ڵ�![]() .��
.��![]() �ǵ�
�ǵ�![]() ����
����![]() ��ĶԳƵ㣬��ֱ��
��ĶԳƵ㣬��ֱ��![]() ��������������ֱ��
��������������ֱ��![]() �Ƿ�����Բ
�Ƿ�����Բ![]() һ����Ψһ�Ĺ����㣿��˵������.
һ����Ψһ�Ĺ����㣿��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ִ����������Ϣ��������Ҫ���ߣ���ͳ�ƣ�ij��˾![]() ��Ա����
��Ա����![]() ����ʹ����������ÿ��ʹ����ʱ����һСʱ���ڵ���
����ʹ����������ÿ��ʹ����ʱ����һСʱ���ڵ���![]() �������Ա��ÿ��ʹ���ŵ�ʱ����һСʱ���ϣ�����Ա���ֳ����꣨����С��
�������Ա��ÿ��ʹ���ŵ�ʱ����һСʱ���ϣ�����Ա���ֳ����꣨����С��![]() �꣩�����꣨���䲻С��
�꣩�����꣨���䲻С��![]() �꣩�����Σ���ôʹ���ŵ�����
�꣩�����Σ���ôʹ���ŵ�����![]() ��������.���涨��ÿ��ʹ����ʱ����һСʱ����Ϊ����ʹ���ţ���ô����ʹ���ŵ�Ա����
��������.���涨��ÿ��ʹ����ʱ����һСʱ����Ϊ����ʹ���ţ���ô����ʹ���ŵ�Ա����![]() ��������.
��������.
��1����Ҫ����ù�˾ʹ���ŵ�Ա������ʹ����������Ĺ�ϵ���г�![]() ��������
��������
������ | ������ | �ܼ� | |
����ʹ���� | |||
������ʹ���� | |||
�ܼ� |
��2���������������������жϣ��Ƿ��аٷ�֮![]() �İ�����Ϊ������ʹ�����������йء���
�İ�����Ϊ������ʹ�����������йء���
| 0.010 | 0.001 |
| 6.635 | 10.828 |
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A=60�㣬AB=3��AC=2���� ![]() =2
=2 ![]() ��
�� ![]() =��
=�� ![]() ��
�� ![]() ���ˡ�R������
���ˡ�R������ ![]() =��4����˵�ֵΪ ��
=��4����˵�ֵΪ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com