
【题目】在直角坐标系中,曲线C的参数方程: ![]() ,直线l的参数方程为
,直线l的参数方程为 ![]() .
.
(1)若直线l与曲线C只有一个公共点,求实数a;
(2)若点P,Q分别为直线l与曲线C上的动点,若 ![]() ,求实数a.
,求实数a.
【答案】
(1)解:∵曲线C的参数方程: 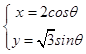 ,
,
∴曲线C的普通方程为 ![]() =1,
=1,
∵直线l的参数方程为 ![]() ,
,
∴直线l的普通方程为x+2y﹣a﹣2=0,
联立 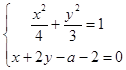 ,得16y2﹣(12a+24)y+3a2+12a=0,
,得16y2﹣(12a+24)y+3a2+12a=0,
∵直线l与曲线C只有一个公共点,
∴△=[﹣(12a+24)]2﹣4×16×(3a2+12a)=﹣a2﹣4a+12=0,
解得a=2或a=﹣6
(2)解:设Q(2cosθ, ![]() ),
),
点Q到直线l的距离d= 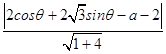 =
= ![]() |4sin(
|4sin( ![]() )﹣a﹣2|,
)﹣a﹣2|,
∵点P,Q分别为直线l与曲线C上的动点, ![]() ,
,
∴当sin( ![]() )=1时,|PQ|min=
)=1时,|PQ|min= ![]() |2﹣a|=
|2﹣a|= ![]() ,
,
解得a=1或a=3
【解析】(1)由曲线C的参数方程求出曲线C的普通方程为 ![]() =1,由直线l的参数方程求出直线l的普通方程为x+2y﹣a﹣2=0,联立
=1,由直线l的参数方程求出直线l的普通方程为x+2y﹣a﹣2=0,联立 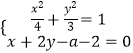 ,得16y2﹣(12a+24)y+3a2+12a=0,由直线l与曲线C只有一个公共点,利用根的判别式为0,能求出a.(2)设Q(2cosθ,
,得16y2﹣(12a+24)y+3a2+12a=0,由直线l与曲线C只有一个公共点,利用根的判别式为0,能求出a.(2)设Q(2cosθ, ![]() ),求出点Q到直线l的距离d=
),求出点Q到直线l的距离d= ![]() |4sin(
|4sin( ![]() )﹣a﹣2|,由题意知当sin(
)﹣a﹣2|,由题意知当sin( ![]() )=1时,|PQ|min=
)=1时,|PQ|min= ![]() |2﹣a|=
|2﹣a|= ![]() ,由此能求出a.
,由此能求出a.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,且DM=2 ![]() .
. 
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求点B到平面DOM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,当
,当![]() 时,恒有
时,恒有![]() .当
.当![]() 时,
时, ![]() .
.
(Ⅰ)求证: ![]() 是奇函数;
是奇函数;
(Ⅱ)若![]() ,试求
,试求![]() 在区间
在区间![]() 上的最值;
上的最值;
(Ⅲ)是否存在![]() ,使
,使![]() 对于任意
对于任意![]() 恒成立?若存在,求出实数
恒成立?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2). 
(1)设∠BOP=α(rad),将S表示为α的函数;
(2)确定点P的位置,使绿化面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx与g(x)=log4(a2x﹣![]() a),其中f(x)是偶函数.
a),其中f(x)是偶函数.
(1)求实数k的值;
(2)求函数g(x)的定义域;
(3)若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)= ![]() (a>0且a≠1).
(a>0且a≠1).
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)设a=![]() ,解不等式f(x)>0.
,解不等式f(x)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com