
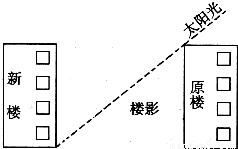
 如图所示,位于北纬36°34′的某疗养院,打算在一幢20米高的楼房北面新建一幢楼房.因为疗养的需要,要求高楼的每一层一年四季都能晒到太阳.
如图所示,位于北纬36°34′的某疗养院,打算在一幢20米高的楼房北面新建一幢楼房.因为疗养的需要,要求高楼的每一层一年四季都能晒到太阳.| 20 |
| tan30° |


科目:高中数学 来源: 题型:
 已知位于y轴右侧的圆C与y相切于点P(0,1),与x轴相交于点A、B,且被x轴分成的两段弧之比为1﹕2(如图所示).
已知位于y轴右侧的圆C与y相切于点P(0,1),与x轴相交于点A、B,且被x轴分成的两段弧之比为1﹕2(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:
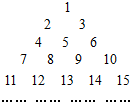 (2006•广州模拟)把正整数排列成如图所示的数阵.
(2006•广州模拟)把正整数排列成如图所示的数阵.查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷E(十三)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com