Question

如下图，设P为长方形ABCD所在平面外一点，M、N分别为AB、PD上的点，且＝，求证：直线MN∥平面PBC．

Answer 1

答案：
解析：

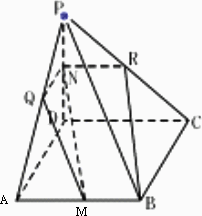
分析：要证直线MN∥平面PBC，只需证明MN∥平面PBC内的一条直线或MN所在的某个平面∥平面PBC． 　　证法一：过N作NR∥DC交PC于点R，连结RB，依题意得 　　＝＝＝＝NR＝MB． 　　∵NR∥DC∥AB， 　　∴四边形MNRB是平行四边形．∴MN∥RB． 　　又∵RB平面PBC，∴直线MN∥平面PBC． 　　证法二：过N作NQ∥AD交PA于点Q，连结QM， 　　∵＝＝，∴QM∥PB．又NQ∥AD∥BC， 　　∴平面MQN∥平面PBC．∴直线MN∥平面PBC． 　　证法三：过N作NR∥DC交PC于点R，连结RB， 　　依题意有＝＝， 　　∴＝，＝＋＋＝． 　　∴MN∥RB．又∵RB平面PBC， 　　∴直线MN∥平面PBC