
【题目】已知α,β∈(0, ![]() )且sin(α+2β)=
)且sin(α+2β)= ![]()
(1)若α+β= ![]() ,求sinβ的值;
,求sinβ的值;
(2)若sinβ= ![]() ,求cosα的值.
,求cosα的值.
【答案】
(1)解:∵α,β∈(0, ![]() ),sin(α+2β)=
),sin(α+2β)= ![]() ,α+β=
,α+β= ![]() ,
,
∴cos(α+2β)=﹣ ![]() ,
,
∴sinβ=sin[(α+2β)﹣ ![]() ]=
]= ![]() ﹣(﹣
﹣(﹣ ![]() )×
)× ![]() =
= ![]()
(2)解:∵sinβ= ![]() ,β∈(0,
,β∈(0, ![]() ),
),
∴cosβ= ![]() ,
,
∴sin2β=2sinβcosβ= ![]() ,cos2β=2cos2β﹣1=﹣
,cos2β=2cos2β﹣1=﹣ ![]() ,
,
∴2β∈( ![]() ,π),
,π),
又∵α,β∈(0, ![]() ),sin(α+2β)=
),sin(α+2β)= ![]() ,
,
∴cos(α+2β)=﹣ ![]() ,
,
∴cosα=cos(α+2β﹣2β)=(﹣ ![]() )×(﹣
)×(﹣ ![]() )+
)+ ![]() =
= ![]()
【解析】(1)由已知利用同角三角函数基本关系式可求cos(α+2β)的值,由β=(α+2β)﹣ ![]() ,利用两角差的正弦函数公式即可计算得解.(2)由已知利用同角三角函数基本关系式可求cosβ,进而利用倍角公式可求sin2β,cos2β的值,结合范围2β∈(
,利用两角差的正弦函数公式即可计算得解.(2)由已知利用同角三角函数基本关系式可求cosβ,进而利用倍角公式可求sin2β,cos2β的值,结合范围2β∈( ![]() ,π),可求cos(α+2β)的值,由α=α+2β﹣2β,利用两角差的余弦函数公式即可计算得解.
,π),可求cos(α+2β)的值,由α=α+2β﹣2β,利用两角差的余弦函数公式即可计算得解.
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识,掌握两角和与差的正弦公式:![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sin(x+
sin(x+ ![]() )cos(x﹣
)cos(x﹣ ![]() )﹣cos2x﹣
)﹣cos2x﹣ ![]() .
.
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)在[﹣ ![]() ,
, ![]() π]上的最大值.
π]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为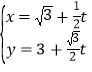 (t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2
(t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2![]() cosθ.
cosθ.
(1)求直线l的普通方程与曲线C的直角坐标方程。
(2)求出直线l与曲线C相交后的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两曲线f(x)=cosx,g(x)= ![]() sinx,x∈(0,
sinx,x∈(0, ![]() )相交于点A.若两曲线在点A处的切线与x轴分别相交于B,C两点,则线段BC的长为 .
)相交于点A.若两曲线在点A处的切线与x轴分别相交于B,C两点,则线段BC的长为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线x﹣2y+2与圆C:x2+y2﹣4y+m=0相交,截得的弦长为 ![]()
(1)求圆C的方程;
(2)过点M(﹣1,0)作圆C的切线,求切线的直线方程;
(3)若抛物线y=x2上任意三个不同的点P、Q、R,且满足直线PQ和PR都与圆C相切,判断直线QR与圆C的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为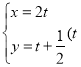 为参数),直线
为参数),直线![]() 和圆
和圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 的任意一点.
的任意一点.
(1)求圆心的极坐标;
(2)求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )

A. 144种 B. 72种 C. 64种 D. 84种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com