
【题目】下面左图是我省某地斜拉式大桥的图片,合肥一中学数学兴趣小组对大桥有关数据进行了测量,并将其简化为右图所示.其中桥塔AB,CD与桥面AC垂直,若![]() .
.

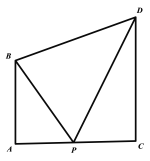
(1)当![]() 时,试确定点P在线段AC上的位置,并写出求解过程;
时,试确定点P在线段AC上的位置,并写出求解过程;
(2)要使得![]() 达到最大,试问点P在线段AC上何处?请写出求解过程.
达到最大,试问点P在线段AC上何处?请写出求解过程.
科目:高中数学 来源: 题型:
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
|
|
|
|
环保部门对企业评估完成后,随机抽取了![]() 家企业的评估得分(
家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是
表示模糊不清的两个数字,但知道样本评估得分的平均数是![]() .
.
(1)现从样本外的数百个企业评估得分中随机抽取![]() 个,若以样本中频率为概率,求该家企业的奖励不少于
个,若以样本中频率为概率,求该家企业的奖励不少于![]() 万元的概率;
万元的概率;
(2)现从样本“不合格”、“合格”、“良好”三个等级中,按分层抽样的方法抽取![]() 家企业,再从这
家企业,再从这![]() 家企业随机抽取
家企业随机抽取![]() 家,求这两家企业所获奖励之和不少于
家,求这两家企业所获奖励之和不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位准备购买三台设备,型号分别为![]() 已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元,也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应购买的易耗品的件数.该单位调查了这三种型号的设备各60台,调査每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元,也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应购买的易耗品的件数.该单位调查了这三种型号的设备各60台,调査每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
型号A | 30 | 30 | 0 | |
频数 | 型号B | 20 | 30 | 10 |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中![]() 三台设备使用的易耗品总数超过21件的概率;
三台设备使用的易耗品总数超过21件的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身房为了解运动健身减肥的效果,调查了![]() 名肥胖者健身前(如直方图(1)所示)后(如直方图(2)所示)的体重(单位:
名肥胖者健身前(如直方图(1)所示)后(如直方图(2)所示)的体重(单位:![]() )变化情况:
)变化情况:
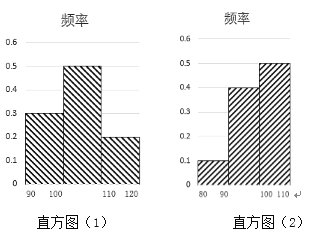
对比数据,关于这![]() 名肥胖者,下面结论正确的是( )
名肥胖者,下面结论正确的是( )
A.他们健身后,体重在区间![]() 内的人数较健身前增加了
内的人数较健身前增加了![]() 人
人
B.他们健身后,体重原在区间![]() 内的人员一定无变化
内的人员一定无变化
C.他们健身后,![]() 人的平均体重大约减少了
人的平均体重大约减少了![]()
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
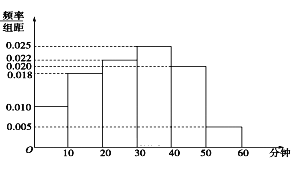
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的22列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
附:![]() .
.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为矩形,点A、E、B、F共面,且![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 90°.
90°.

(Ⅰ)若平面ABCD![]() 平面AEBF,证明平面BCF
平面AEBF,证明平面BCF![]() 平面ADF;
平面ADF;
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面CDF,若存在,求出此时三棱锥G-ABE与三棱锥G-ADF的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
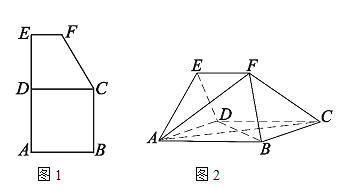
【题目】如图1,平面五边形![]() 是由边长为2的正方形
是由边长为2的正方形![]() 与上底为1,高为
与上底为1,高为![]() 直角梯形
直角梯形![]() 组合而成,将五边形
组合而成,将五边形![]() 沿着
沿着![]() 折叠,得到图2所示的空间几何体,其中
折叠,得到图2所示的空间几何体,其中![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是中国古代的著名数学著作,该书表明:至迟于公元5世纪,中国已经系统掌握等差数列的相关理论,该书上卷22题又“女工善织问题”:“今有女善织,日益功疾,初日织五尺,今一月曰织九匹三丈,问日益几何?”,大概意思是:有一个女工人善于织布,每天织布的尺数越来越多且成等差数列,第一天知5尺,30天共织九匹三丈,问每天增加的织布数目是多少寸?答案是__________寸.(注:当时一匹为四丈,一丈为十尺,一尺为十寸,结果四舍五入精确到寸)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com