练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    椭圆的两焦点把椭圆的对称轴上夹在两准线间的线段三等分，则椭圆的离心率为________．


    分析：确定椭圆的两准线间的距离、两焦点间的距离，利用两焦点三等分椭圆两准线间的距离，建立方程，即可求得椭圆的离心率．
    解答：两准线间的距离为，两焦点间的距离2c，
    ∵两焦点三等分椭圆两准线间的距离，
    ∴2c=•，即：6c2=2a2，
    ∴e==
    故答案为．
    点评：本题考查椭圆的性质，考查学生的计算能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    把一颗骰子投掷两次，记第一次出现的点数为a2，第二次出现的点数为b2（其中a＞0，b＞0）．试求：
    （Ⅰ）方程
    x2
    a2
    +
    y2
    b2
    =1    表示焦点在x轴上的椭圆的概率；
    （Ⅱ）方程
    x2
    a2
    -
    y2
    b2
    =1    表示离心率为2的双曲线的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•浦东新区二模）（1）设椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1    与双曲线C2：9x2-
    9y2
    8
    =1    有相同的焦点F1、F2，M是椭圆C1与双曲线C2的公共点，且△MF1F2的周长为6，求椭圆C1的方程；
    我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．
    （2）如图，已知“盾圆D”的方程为y2=
    4x            (0≤x≤3)
    -12(x-4)  (3＜x≤4)
    ．设“盾圆D”上的任意一点M到F（1，0）的距离为d1，M到直线l：x=3的距离为d2，求证：d1+d2为定值； 
    （3）由抛物线弧E1：y2=4x（0≤x≤
    2
    3
    ）与第（1）小题椭圆弧E2：
    x2
    a2
    +
    y2
    b2
    =1    （
    2
    3
    ≤x≤a    ）所合成的封闭曲线为“盾圆E”．设过点F（1，0）的直线与“盾圆E”交于A、B两点，|FA|=r1，|FB|=r2且∠AFx=α（0≤α≤π），试用cosα表示r1；并求
    r1
    r2
    的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：022

    给出下列四个命题：

    ①椭圆=1上一点P到左、右焦点距离之比为2：3，则P上到右准线的距离是10；

    ②椭圆=1的离心率是；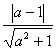

    ③将椭圆=1绕其左焦点按顺时针方向旋转，则所得椭圆的准线方程是y=和y=－；

    ④P是椭圆4x2+9y2－36=0上一点，F1、F2是椭圆的两个焦点，cos∠F1PF2的最小值是。

    其中正确命题的序号是________(把你认为正确命题的序号都填上)。

     

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：022

    给出下列四个命题：

    ①椭圆=1上一点P到左、右焦点距离之比为2：3，则P上到右准线的距离是10；

    ②椭圆=1的离心率是；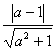

    ③将椭圆=1绕其左焦点按顺时针方向旋转，则所得椭圆的准线方程是y=和y=－；

    ④P是椭圆4x2+9y2－36=0上一点，F1、F2是椭圆的两个焦点，cos∠F1PF2的最小值是。

    其中正确命题的序号是________(把你认为正确命题的序号都填上)。

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年安徽省巢湖市高三（上）质量检测数学试卷（理科）（解析版） 题型：填空题

    给出下列命题：
    ①已知椭圆的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
    ②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
    ③若过双曲线C：的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
    ④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
    其中正确命题的序号是    ．（把你认为正确命题的序号都填上）

    查看答案和解析>>

    同步练习册答案