
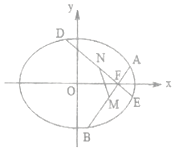
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.分析 (1)利用已知条件列出方程组,求出a,b即可得到椭圆方程.
(2))根据$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{CN}=\frac{1}{2}\overrightarrow{CD}$可知,M,N分别为AB,DE的中点,点A(x1,y1),B(x2,y2),直线AB的方程为x=my+1,不妨设m>0,联立椭圆C有(m2+2)y2+2my-1=0,根据韦达定理弦长公式,转化求解三角形的面积,通过换元法以及基本不等式求解三角形的最值.
解答 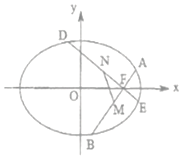 解:(1)根据条件有$\left\{\begin{array}{l}{a^2}=2{b^2}\\ \frac{1}{{2{a^2}}}+\frac{3}{{4{b^2}}}=1\end{array}\right.$,解得a2=2,b2=1,所以椭圆$C:\frac{x^2}{2}+{y^2}=1$.
解:(1)根据条件有$\left\{\begin{array}{l}{a^2}=2{b^2}\\ \frac{1}{{2{a^2}}}+\frac{3}{{4{b^2}}}=1\end{array}\right.$,解得a2=2,b2=1,所以椭圆$C:\frac{x^2}{2}+{y^2}=1$.
(2)根据$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{CN}=\frac{1}{2}\overrightarrow{CD}$可知,M,N分别为AB,DE的中点,且直线AB,DE斜率均存在且不为0,
现设点A(x1,y1),B(x2,y2),直线AB的方程为x=my+1,
不妨设m>0,联立椭圆C有(m2+2)y2+2my-1=0,
根据韦达定理得:${y_1}+{y_2}=-\frac{2m}{{{m^2}+2}}$,${x_1}+{x_2}=m({y_1}+{y_2})+2=\frac{4}{{{m^2}+2}}$,$M(\frac{2}{{{m^2}+2}},\frac{-m}{{{m^2}+2}})$,$|MF|=\frac{{m\sqrt{{m^2}+1}}}{{{m^2}+2}}$,
同理可得$|NF|=\frac{{|-\frac{1}{m}|\sqrt{{{(-\frac{1}{m})}^2}+1}}}{{{{(-\frac{1}{m})}^2}+2}}$,
所以△MNF面积${S_{△MNF}}=\frac{1}{2}|MF||NF|=\frac{{m+\frac{1}{m}}}{{4{{(m+\frac{1}{m})}^2}+2}}$,
现令$t=m+\frac{1}{m}≥2$,
那么${S_{△MNF}}=\frac{t}{{4{t^2}+2}}=\frac{1}{{4t+\frac{2}{t}}}≤\frac{1}{9}$,
所以当t=2,m=1时,△MNF的面积取得最大值$\frac{1}{9}$.
点评 本题考查椭圆的简单性质以及椭圆方程的求法,直线与椭圆的位置关系的综合应用,三角形面积的最值的求法,基本不等式以及换元法的应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
| 轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥4或k≤-4 | B. | $k≥\sqrt{2}$或$k≤-2\sqrt{2}$ | C. | $k=±2\sqrt{3}$ | D. | $k=±2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2α-β=\frac{π}{4}$ | B. | $2α+β=\frac{π}{4}$ | C. | $α-β=\frac{π}{4}$ | D. | $α+β=\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
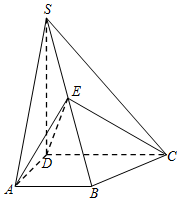 如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com