
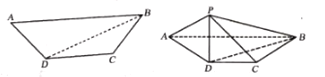
【题目】已知四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() 沿对角线将
沿对角线将![]() 旋转,使得点
旋转,使得点![]() 至点
至点![]() 的位置,此时满足
的位置,此时满足![]() .
.
(1)判断![]() 的形状,并证明;
的形状,并证明;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cosx,C2:y=sin(2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:家占
.美国高中生答题情况是:家占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .为了考察高中生的“恋家(在家里感到最幸福)”是否与国别有关,构建了如下
.为了考察高中生的“恋家(在家里感到最幸福)”是否与国别有关,构建了如下![]() 列联表.
列联表.
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从中国高中生的学生中以“是否恋家”为标准采用分层抽样的方法,随机抽取了5人,再从这5人中随机抽取2人.若所选2名学生中的“恋家”人数为![]() ,求随机变量
,求随机变量![]() 的分布列及期望.
的分布列及期望.
附: 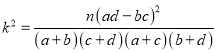 ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 各项均为正数,
各项均为正数, ![]() ,
, ![]() ,且
,且![]() 对任意
对任意![]() 恒成立,记
恒成立,记![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)证明:对任意正实数![]() ,
, ![]() 成等比数列;
成等比数列;
(3)是否存在正实数![]() ,使得数列
,使得数列![]() 为等比数列.若存在,求出此时
为等比数列.若存在,求出此时![]() 和
和![]() 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级240名学生进行一次测试.共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如表所示:
为参加测试的总人数.现对某校高三年级240名学生进行一次测试.共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如表所示:

测试后,随机抽取了 20名学生的答题数据进行统计,结果如下

(1)根据题中数据,估计这240名学生中第5题的实测答对人数;
(2)从抽取的20名学生中再随机抽取2名学生,记这2名学生中第5题答对的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度
题的预估难度![]() .规定:若
.规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.试据此判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.试据此判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() )在点
)在点![]() 处的切线斜率为1.
处的切线斜率为1.
(1)用![]() 表示
表示![]() ;
;
(2)设![]() ,若
,若![]() 对定义域内的
对定义域内的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的前提下,如果![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com