
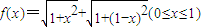 的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的图象的对称轴是 ;函数g(x)=4f(x)-9的零点的个数是 .
的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的图象的对称轴是 ;函数g(x)=4f(x)-9的零点的个数是 .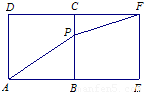
 的解的个数.
的解的个数. ;
; .故函数g(x)=4f(x)-9的零点的个数就是f(x)=
.故函数g(x)=4f(x)-9的零点的个数就是f(x)= 的解的个数.
的解的个数. 的解有2个,
的解有2个, ;2
;2

科目:高中数学 来源:2013-2014学年上海市十二校高三12月联考理科数学试卷(解析版) 题型:选择题
某同学为了研究函数 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为 的正方形
的正方形 和
和 ,点
,点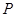 是边
是边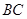 上的一个动点,设
上的一个动点,设 ,则
,则 .那么可推知方程
.那么可推知方程 解的个数是( )
解的个数是( )

(A) . (B)
. (B) . (C)
. (C) .
(D)
.
(D) .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三5月模拟考试理科数学试卷(解析版) 题型:填空题
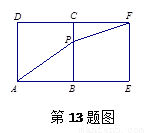
.某同学为研究函数 的性质,构造了如下图所示的两个边长为1的正方形
的性质,构造了如下图所示的两个边长为1的正方形 和
和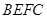 ,点
,点 是边
是边 上的一个动点,设
上的一个动点,设 ,则
,则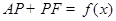 . 请你参考这些信息,推知函数
. 请你参考这些信息,推知函数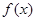 的图象的对称轴是 .
的图象的对称轴是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某同学为研究函数
某同学为研究函数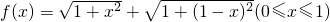 的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的图象的对称轴是________;函数g(x)=4f(x)-9的零点的个数是________.
的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的图象的对称轴是________;函数g(x)=4f(x)-9的零点的个数是________.查看答案和解析>>
科目:高中数学 来源:河北省模拟题 题型:填空题

 的性质,构造了如图所示的两个边长为1的正方形
的性质,构造了如图所示的两个边长为1的正方形 和
和 ,点
,点 是边
是边 上的一个动点,设
上的一个动点,设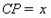 ,则
,则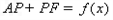 . 请你参考这些信息,推知函数
. 请你参考这些信息,推知函数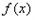 的图象的对称轴是( );函数
的图象的对称轴是( );函数 的零点的个数是( )
的零点的个数是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com