
【题目】在直角坐标平面上的一列点![]() 简记为
简记为![]() ,若由
,若由![]() 构成的数列
构成的数列![]() 满足
满足![]() ,(其中
,(其中![]() 是与
是与![]() 轴正方向相同的单位向量),则称
轴正方向相同的单位向量),则称![]() 为“
为“![]() 点列”.
点列”.
(1)试判断:![]() ,...是否为“
,...是否为“![]() 点列”?并说明理由.
点列”?并说明理由.
(2)若![]() 为“
为“![]() 点列”,且点
点列”,且点![]() 在点
在点![]() 的右上方.任取其中连续三点
的右上方.任取其中连续三点![]() ,判断
,判断![]() 的形状(锐角,直角,钝角三角形),并证明.
的形状(锐角,直角,钝角三角形),并证明.
(3)若![]() 为“
为“![]() 点列”,正整数
点列”,正整数![]() 满足:
满足:![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)是“![]() 点列”,理由见解析;(2)钝角三角形,证明见解析;(3)证明见解析
点列”,理由见解析;(2)钝角三角形,证明见解析;(3)证明见解析
【解析】
(1)根据所给的![]() 个点的坐标,观察出数列
个点的坐标,观察出数列![]() 的通项公式,把数列
的通项公式,把数列![]() 的通项代入新定义的数列
的通项代入新定义的数列![]() ,验证数列
,验证数列![]() 满足
满足![]() ,得到
,得到![]() 是
是![]() 点列的结论.
点列的结论.
(2)用所给的三个点构造三个向量,写出三个向量的坐标,问题转化为向量夹角的大小问题,判断出两个向量的数量积小于零,得到两个向量所成的角是钝角,得到结果.
(3)本题是要求判断两组向量的数量积的大小,根据两个数列各自的项之间的大小关系,即可得到向量的数量积之间的关系.
解:(1)由题意可知![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
∴![]() 是
是![]() 点列;
点列;
(2)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∵点![]() 在点
在点![]() 的右上方,
的右上方,![]() ,
,
∵![]() 是
是![]() 点列,
点列,![]() ,
,![]() ,则
,则![]() ,
,
![]() 为钝角,
为钝角,![]() 为钝角三角形;
为钝角三角形;
(3)![]() ,
,![]() ①
①![]() ②
②
同理![]() ③
③
由于![]() 是
是![]() 点列,于是
点列,于是![]() ④
④
由①、②、③、④可推得![]() ,
,![]() ,
,
又由(1)知![]()
![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:
【题目】连结圆周上九个不同点的36条弦要么染成红色,要么染成蓝色,我们称它们为“红边”或“蓝边”.假定由这九个点中每三个点为顶点的三角形中都含有“红边”.证明:这九个点中存在四个点,两两连结的六条边都是红边.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
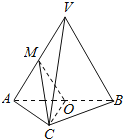
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体,关于其结构特征,下列说法不正确的是
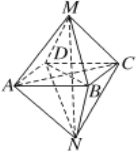
A. 该几何体是由两个同底的四棱锥组成的几何体
B. 该几何体有12条棱、6个顶点
C. 该几何体有8个面,并且各面均为三角形
D. 该几何体有9个面,其中一个面是四边形,其余均为三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋有![]() 个白球,
个白球,![]() 个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为
个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为![]() ,
,![]() ,
,![]() ,
,![]() 的抽屉内.
的抽屉内.
(1)求编号为![]() 的抽屉内放黑球的概率;
的抽屉内放黑球的概率;
(2)口袋中的球放入抽屉后,随机取出两个抽屉中的球,求取出的两个球是一黑一白的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分) 如图,![]() 的外接圆
的外接圆![]() 的半径为
的半径为![]() ,
,![]() 所在的平面,
所在的平面,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
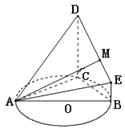
(1)求证:平面ADC![]() 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为![]() ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的是( )
A.半圆弧以其直径为轴旋转一周所形成的曲面叫做球
B.直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体
D.用一个平面截圆锥底面与截面组成的部分是圆台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com