
【题目】在直三棱柱ABC — A1B1C1中,AB=AC,BB1=BC,点P,Q,R分别是棱BC,CC1,B1C1的中点.
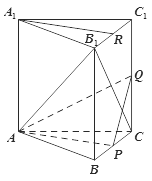
(1)求证:A1R//平面APQ;
(2)求证:直线B1C⊥平面APQ.
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】某地方政府召开全面展开新旧动能转换重大工程动员大会,动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前、后生产的大量产品中各抽取了200件作为样本,检测一项质量指标值.若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
内的产品视为合格品,否则为不合格品.如图所示的是设备改造前样本的频率分布直方图.
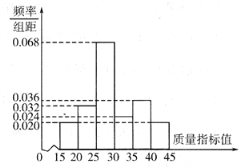
(1)若设备改造后样本的该项质量指标值服从正态分布![]() ,求改造后样本中不合格品的件数;
,求改造后样本中不合格品的件数;
(2)完成下面2×2列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量标值与设备改造有关.
0 | 设备改造前 | 设备改造后 | 合计 |
合格品件数 | |||
不合格品件数 | |||
合计 |
附参考公式和数据:
若![]() ,则
,则![]() ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
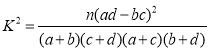
查看答案和解析>>
科目:高中数学 来源: 题型:
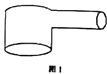
【题目】管道清洁棒是通过在管道内释放清洁剂来清洁管道内壁的工具,现欲用清洁棒清洁一个如图1所示的圆管直角弯头的内壁,其纵截面如图2所示,一根长度为![]() 的清洁棒在弯头内恰好处于
的清洁棒在弯头内恰好处于![]() 位置(图中给出的数据是圆管内壁直径大小,
位置(图中给出的数据是圆管内壁直径大小,![]() ).
).

(1)请用角![]() 表示清洁棒的长
表示清洁棒的长![]() ;
;
(2)若想让清洁棒通过该弯头,清洁下一段圆管,求能通过该弯头的清洁棒的最大长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是 (
(![]() 是参数).以坐标原点
是参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,其倾斜角为
,其倾斜角为![]() .
.
(Ⅰ)证明直线![]() 恒过定点
恒过定点![]() ,并写出直线
,并写出直线![]() 的参数方程;
的参数方程;
(Ⅱ)在(Ⅰ)的条件下,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,并解答.
这三个条件中任选一个,补充在下面问题中,并解答.
已知等差数列![]() 的公差为
的公差为![]() ,等差数列
,等差数列![]() 的公差为
的公差为![]() .设
.设![]() 分别是数列
分别是数列![]() 的前
的前![]() 项和,且
项和,且![]() , ,
, ,
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 在区间
在区间![]() 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(2)若函数![]() 在区间
在区间![]() 上有两个极值点,求实数a的取值范围;
上有两个极值点,求实数a的取值范围;
(3)若函数![]() 的导函数
的导函数![]() 的图象与函数
的图象与函数![]() 图象有两个不同的交点,求实数a的取值范围.
图象有两个不同的交点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,
(1)若展开式中第5项,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大项
的系数;
(2)若展开式前三项的二项式系数和等于79,求展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com