
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.

(I)求![]() 的值;
的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
【答案】(Ⅰ) ![]() (Ⅱ) 平均数74.9,众数75.14,中位数75;(Ш)
(Ⅱ) 平均数74.9,众数75.14,中位数75;(Ш) ![]()
【解析】
(I)根据频率之和为![]() 列方程,结合
列方程,结合![]() 求出
求出![]() 的值.(II)利用各组中点值乘以频率然后相加,求得平均数.利用中位数是面积之和为
的值.(II)利用各组中点值乘以频率然后相加,求得平均数.利用中位数是面积之和为![]() 的地方,列式求得中位数.以频率分布直方图最高一组的中点作为中位数.(III)先计算出从
的地方,列式求得中位数.以频率分布直方图最高一组的中点作为中位数.(III)先计算出从![]() ,
,![]() 中分别抽取
中分别抽取![]() 人和
人和![]() 人,再利用列举法和古典概型概率计算公式,计算出所求的概率.
人,再利用列举法和古典概型概率计算公式,计算出所求的概率.
解:(I)依题意得![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
(Ⅱ)平均数为![]()
中位数为![]()
众数为![]()
(Ш)依题意,知分数在![]() 的市民抽取了2人,记为
的市民抽取了2人,记为![]() ,分数在
,分数在![]() 的市民抽取了6人,记为1,2,3,4,5,6,
的市民抽取了6人,记为1,2,3,4,5,6,
所以从这8人中随机抽取2人所有的情况为:
![]() ,
,
![]() 共28种,
共28种,
其中满足条件的为![]() ,
,![]() 共13种,设“至少有1人的分数在
共13种,设“至少有1人的分数在![]() ”的事件为
”的事件为![]() ,则
,则![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】九十年代,政府间气候变化专业委员会(IPCC)提供的一项报告指出:使全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐中使CO2浓度增加.据测,1990年、1991年、1992年大气中的CO2浓度分别比1989年增加了1个可比单位、3个可比单位、6个可比单位。若用函数模拟九十年代中每年CO2浓度增加的可比单位数y与年份增加数x的关系,模拟函数可选用二次函数或函数![]() (其中a、b、c为常数).
(其中a、b、c为常数).
(Ⅰ)写出这两个函数的解释式;
(Ⅱ)若知1994年大气中的CO2浓度比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数与1994年的实际数据更接近?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在不为零的常数![]() ,使得函数
,使得函数![]() 对定义域内的任一
对定义域内的任一![]() 均有
均有![]() ,则称函数
,则称函数![]() 为周期函数,其中常数
为周期函数,其中常数![]() 就是函数的一个周期.
就是函数的一个周期.
(Ⅰ)证明:若存在不为零的常数![]() 使得函数
使得函数![]() 对定义域内的任一
对定义域内的任一![]() 均有
均有![]() ,则此函数是周期函数;
,则此函数是周期函数;
(Ⅱ)若定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,试探究此函数在区间
,试探究此函数在区间![]() 内的零点的最少个数.
内的零点的最少个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 的外接圆半径.
的外接圆半径.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)在![]() 中,若
中,若![]() 为钝角,求证:
为钝角,求证:![]() ;
;
(3)给定三个正实数![]() 、
、![]() 、
、![]() ,其中
,其中![]() ,问:
,问:![]() 、
、![]() 、
、![]() 满足怎样的关系时,以
满足怎样的关系时,以![]() 、
、![]() 为边长,
为边长,![]() 为外接圆半径的
为外接圆半径的![]() 不存在,存在一个或存在两个(全等的三角形算作同一个)?在
不存在,存在一个或存在两个(全等的三角形算作同一个)?在![]() 存在的情兄下,用
存在的情兄下,用![]() 、
、![]() 、
、![]() 表示
表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系上一动点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的2倍。
的距离的2倍。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 与点
与点![]() 关于点
关于点![]() 对称,求
对称,求![]() ,
,![]() 两点间距离的最大值。
两点间距离的最大值。
(3)若过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() ,则是否存在直线
,则是否存在直线![]() ,使
,使![]() 取得最大值,若存在,求出此时
取得最大值,若存在,求出此时![]() 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量![]() 单位:吨
单位:吨![]() ,将数据按照
,将数据按照![]() ,
,![]() ,
,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
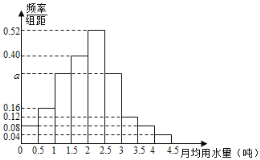
(1)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数![]() 说明理由;
说明理由;
(2)估计居民月均用水量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωxcosωx﹣ ![]() (ω>0)图象的两条相邻对称轴为
(ω>0)图象的两条相邻对称轴为 ![]() .
.
(1)求函数y=f(x)的对称轴方程;
(2)若函数y=f(x)﹣ ![]() 在(0,π)上的零点为x1 , x2 , 求cos(x1﹣x2)的值.
在(0,π)上的零点为x1 , x2 , 求cos(x1﹣x2)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com