
【题目】如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
【答案】D
【解析】
试题分析:首先根据正弦、余弦在(0,π)内的符号特征,确定△A1B1C1是锐角三角形;
然后假设△A2B2C2是锐角三角形,则由cosα=sin(![]() )推导出矛盾;
)推导出矛盾;
再假设△A2B2C2是直角三角形,易于推出矛盾;
最后得出△A2B2C2是钝角三角形的结论.
解:因为△A2B2C2的三个内角的正弦值均大于0,
所以△A1B1C1的三个内角的余弦值也均大于0,则△A1B1C1是锐角三角形.
若△A2B2C2是锐角三角形,由 ,
,
得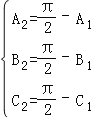 ,
,
那么,![]() ,这与三角形内角和是π相矛盾;
,这与三角形内角和是π相矛盾;
若△A2B2C2是直角三角形,不妨设A2=![]() ,
,
则sinA2=1=cosA1,所以A1在(0,π)范围内无值.
所以△A2B2C2是钝角三角形.
故选D.


科目:高中数学 来源: 题型:
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡数 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算:![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数,![]() .
.
(1)![]() 与
与![]() 是否有较强的线性相关性? 请计算相关系数
是否有较强的线性相关性? 请计算相关系数![]() (精确到
(精确到![]() )说明.
)说明.
(2)并求![]() 关于
关于![]() 的回归方程
的回归方程![]() (
(![]() 和
和![]() 都精确到
都精确到![]() );
);
(3)用(2)中的线性回归模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,
,
①线性相关系数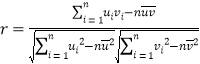 ,通常情况下当
,通常情况下当![]() 大于0.8时,认为两
大于0.8时,认为两
个变量有很强的线性相关性.
②其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
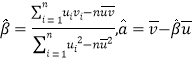 ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
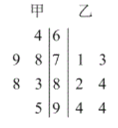
【题目】在桂林市某中学高中数学联赛前的模拟测试中,得到甲、乙两名学生的6次模拟测试成绩(百分制)的茎叶图.分数在85分或85分以上的记为优秀.
(1)根据茎叶图读取出乙学生6次成绩的众数,并求出乙学生的平均成绩以及成绩的中位数;
(2)若在甲学生的6次模拟测试成绩中去掉成绩最低的一次,在剩下5次中随机选择2次成绩作为研究对象,求在选出的成绩中至少有一次成绩记为优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]()
(1)在![]() 轴的正半轴上求一点
轴的正半轴上求一点![]() ,使得以
,使得以![]() 为直径的圆过
为直径的圆过![]() 点,并求该圆的方程;
点,并求该圆的方程;
(2)在(1)的条件下,点![]() 在线段
在线段![]() 内,且
内,且![]() 平分
平分![]() ,试求
,试求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是__________.
①每条直线都有唯一一个倾斜角与之对应,也有唯一一个斜率与之对应;
②倾斜角的范围是:![]() ,且当倾斜角增大时,斜率不一定增大;
,且当倾斜角增大时,斜率不一定增大;
③直线![]() 过点
过点![]() ,且横截距与纵截距相等,则直线
,且横截距与纵截距相等,则直线![]() 的方程一定为
的方程一定为![]() ;
;
④过点![]() ,且斜率为1的直线的方程为
,且斜率为1的直线的方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为菱形,侧面
为菱形,侧面![]() 为等边三角形,且侧面
为等边三角形,且侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求证:平面![]() 平面
平面![]() .
.
(Ⅲ)侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
, ![]() 和一动点
和一动点![]() ,给出下列结论:
,给出下列结论:
①若![]() ,则点
,则点![]() 的轨迹是椭圆;
的轨迹是椭圆;
②若![]() ,则点
,则点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③若![]() ,则点
,则点![]() 的轨迹是圆;
的轨迹是圆;
④若![]() ,则点
,则点![]() 的轨迹关于原点对称;
的轨迹关于原点对称;
⑤若直线![]() 与
与![]() 斜率之积等于
斜率之积等于![]() ,则点
,则点![]() 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).
其中正确的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:
对于任意![]() ,都有
,都有![]() 成立.
成立.
①求数列![]() 的通项公式;
的通项公式;
②设数列![]() ,问:数列
,问:数列![]() 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com