
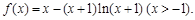
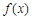 的单调区间;
的单调区间;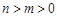 时,
时,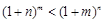 ;
;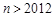 ,且
,且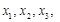 …,
…,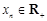 ,
,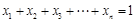 时,
时,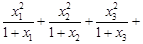 …
…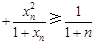
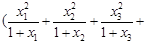 …
…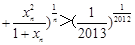 .
.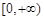 (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析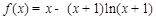 ,有
,有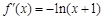 ,………………… 2分
,………………… 2分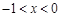 时,
时,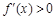 时,
时,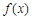 单调递增;
单调递增;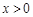 时,
时,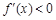 时,
时,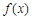 单调递减;
单调递减;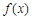 的单调递增区间为
的单调递增区间为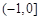 ,单调递减区间为
,单调递减区间为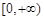 . …… 4分
. …… 4分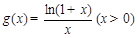 ,
,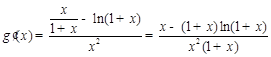 .………………6分
.………………6分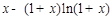 在
在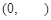 单调递减,
单调递减,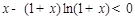 ,即
,即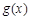 是减函数,
是减函数,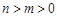 ,所以
,所以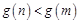 ,得
,得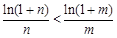 ,
,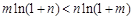 ,故
,故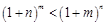 .………………… 8分
.………………… 8分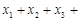 …
…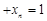 ,及柯西不等式可知,
,及柯西不等式可知,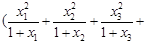 …
…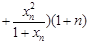
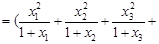 …
…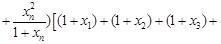 …
…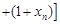
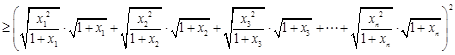
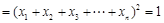 ,
, 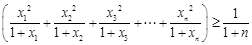 ,……………………11分
,……………………11分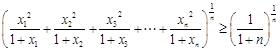 .
. 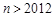 ,由(Ⅱ)可知
,由(Ⅱ)可知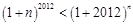 ,
,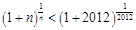 ,即
,即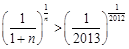 .
.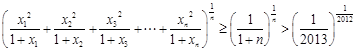 .
.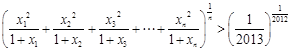 ………………14分
………………14分

科目:高中数学 来源:不详 题型:解答题
 ,在
,在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
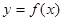 在定义域(-
在定义域(-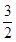 ,3)内可导,其图象如图所示,记
,3)内可导,其图象如图所示,记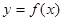 的导函
的导函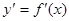 ,则不等式
,则不等式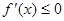 的解集为( )
的解集为( )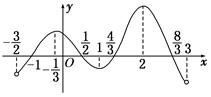
A.[-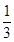 ,1]∪[2,3) ,1]∪[2,3) | B.[-1, ]∪[ ]∪[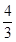 , ,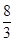 ] ] |
C.[-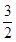 , , ]∪[1,2] ]∪[1,2] | D.[-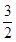 ,- ,-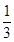 ]∪[ ]∪[ , ,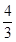 ] ] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com