
【题目】已知函数f(x)=x2﹣2|x|﹣1.
(1)证明函数f(x)是偶函数;
(2)在如图所示的平面直角坐标系中作出函数f(x)的图象.并根据图象写出函数f(x)的单调区间; 
(3)求函数f(x)当x∈[﹣2,4]时的最大值与最小值.
【答案】
(1)证明:∵x∈R,f(﹣x)=(﹣x)2﹣2|﹣x|﹣1=x2﹣2|x|+1=f(x),
∴f(x)是偶函数
(2)解:∵当x≥0时,f(x)=x2﹣2x﹣1,当x<0时,f(x)=x2+2x﹣1,
则函数f(x)图象如图所示
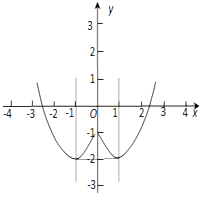
(3)解:由图知当x=﹣1和1时有最小值为﹣2.当x=4时有最大值7
【解析】(1)根据偶函数的定义即可证明,(2)去绝对值,化为分段函数,画图即可,(3)由图象可求出f(x)当x∈[﹣2,4]时的最大值与最小值.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=![]() , AD=1,DC⊥BC,则这块菜地的面积为
, AD=1,DC⊥BC,则这块菜地的面积为 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在(﹣∞,0)上单调递减,且f(2)=0,则不等式xf(x﹣1)>0的解集是( )
A.(﹣3,﹣1)
B.(﹣3,1)∪(2,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣1,0)∪(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的短轴端点和焦点所组成的四边形为正方形,且椭圆
的短轴端点和焦点所组成的四边形为正方形,且椭圆![]() 上任意一点到两个焦点的距离之和为
上任意一点到两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lgx+1(1≤x≤100),则g(x)=f2(x)+f(x2)的值域为( )
A.[﹣2,7]
B.[2,7]
C.[﹣2,14]
D.[2,14]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且(2b-c)cos A=acos C.
(1)求角A的大小;
(2)若a=3,b=2c,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,以椭圆的四个顶点为顶点的四边形的面积为8.
,以椭圆的四个顶点为顶点的四边形的面积为8.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.若
的左上方.若![]() ,且直线
,且直线![]() ,
, ![]() 分别与
分别与![]() 轴交于
轴交于![]() ,
, ![]() 点,求线段
点,求线段![]() 的长度.
的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com