
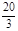 ,椭圆C2的方程为
,椭圆C2的方程为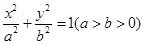 ,C2的离心率为
,C2的离心率为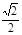 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求: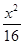 +
+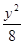 =1。
=1。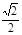 ,得
,得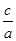 =
=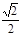 ,a2=2c2,b2=c2。
,a2=2c2,b2=c2。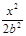 +
+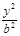 =1。又设A(x1,y1),B(x2,y2)。由圆心为(2,1),得x1+x2=4,y1+y2=2。
=1。又设A(x1,y1),B(x2,y2)。由圆心为(2,1),得x1+x2=4,y1+y2=2。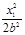 +
+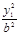 =1,
=1,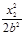 +
+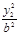 =1,两式相减,得
=1,两式相减,得 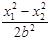 +
+ =0。
=0。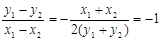
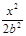 +
+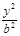 =1,得3x2-12x+18-2b2=0
=1,得3x2-12x+18-2b2=0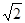 |x1-x2|=
|x1-x2|=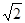
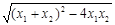 =
=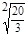 ,得
,得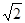 ·
·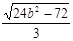 =
=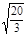 。
。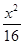 +
+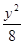 =1。
=1。

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com