[题目]如图.三棱锥中.底面△是边长为2的正三角形..底面.点分别为.的中点.(1)求证:平面平面,(2)在线段上是否存在点.使得三棱锥体积为?若存在.确定点的位置,若不存在.请说明理由. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，三棱锥中，底面△是边长为2的正三角形，，底面，点分别为，的中点.

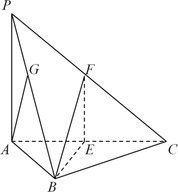
（1）求证：平面平面；

（2）在线段上是否存在点，使得三棱锥体积为？若存在，确定点的位置；若不存在，请说明理由.

【答案】（1）证明见解析.（2）存在，为中点.

【解析】

（1）由底面推出，结合可推出平面，线面垂直推出面面垂直；（2）过G作，由面面垂直的性质证明平面ABC，再利用等体积法由即可求得，根据线面垂直的性质及中位线的性质即可求得点G的位置.

（1）因为底面，底面，所以，

因为△是等边三角形且E为AC的中点，所以，

又，平面PAC，平面PAC，

所以平面，

因为平面，所以平面平面；

（2）过G作,

平面ABC，平面PAB，平面PAB平面ABC

又平面PAB平面ABC=AB，平面ABC,

，，

平面ABC，平面ABC，,

，为PB中点.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知数列的前项和为，且．

（1）若为等差数列，且

①求该等差数列的公差；

②设数列满足，则当为何值时，最大？请说明理由；

（2）若还同时满足：

①为等比数列;

②；

③对任意的正整数存在自然数，使得、、依次成等差数列，试求数列的通项公式．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内，每售出吨该商品可获利润万元，未售出的商品，每吨亏损万元.根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了吨该商品.现以（单位：吨，）表示下一个销售季度的市场需求量，（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润.

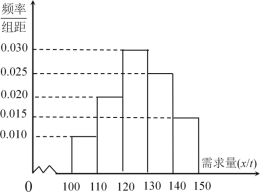
（1）将表示为的函数，求出该函数表达式；

（2）根据直方图估计利润不少于57万元的概率；

（3）根据频率分布直方图，估计一个销售季度内市场需求量的平均数与中位数的大小（保留到小数点后一位）.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标中，圆，圆。

(Ⅰ)在以O为极点，x轴正半轴为极轴的极坐标系中，分别写出圆的极坐标方程，并求出圆的交点坐标(用极坐标表示)；

(Ⅱ)求圆的公共弦的参数方程。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数的图像是由函数的图像经如下变换得到：先将图像上所有点的纵坐标伸长到原来的2倍（横坐标不变），再将所得到的图像向右平移个单位长度.

（Ⅰ）求函数的解析式，并求其图像的对称轴方程；

（Ⅱ）已知关于的方程在内有两个不同的解．

（1）求实数m的取值范围；

（2）证明：

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在新冠病毒肆虐全球的大灾难面前，中国全民抗疫，众志成城，取得了阶段性胜利，为世界彰显了榜样力量.为庆祝战疫成功并且尽快恢复经济，某网络平台的商家进行有奖促销活动，顾客购物消费每满600元，可选择直接返回60元现金或参加一次答题返现，答题返现规则如下：电脑从题库中随机选出一题目让顾客限时作答，假设顾客答对的概率都是0.4，若答对题目就可获得120元返现奖励，若答错，则没有返现.假设顾客答题的结果相互独立.

（1）若某顾客购物消费1800元，作为网络平台的商家，通过返现的期望进行判断，是希望顾客直接选择返回180元现金，还是选择参加3次答题返现？

（2）若某顾客购物消费7200元并且都选择参加答题返现，请计算该顾客答对多少次概率最大，最有可能返回多少现金？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】甲、乙二人进行一次象棋比赛，每局胜者得1分，负者得0分（无平局），约定一方得4分时就获得本次比赛的胜利并且比赛结束，设在每局比赛中，甲获胜的概率为，乙获胜的概率为，各局比赛结果相互独立，已知前3局中，甲得1分，乙得2分.