
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)若函数![]() 在
在![]() 上恒有意义,求
上恒有意义,求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]() ?若存在求出
?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据![]() 在
在![]() 上恒有意义,则
上恒有意义,则![]() 在
在![]() 上恒成立.讨论对称轴的位置,即可求得
上恒成立.讨论对称轴的位置,即可求得![]() 的取值范围.
的取值范围.
(2)讨论![]() 与
与![]() 两种情况,结合复函函数单调性即可判断是否符合单调递增.再根据最大值为
两种情况,结合复函函数单调性即可判断是否符合单调递增.再根据最大值为![]() ,代入
,代入![]() 的值,解方程即可求解.
的值,解方程即可求解.
(1)函数![]() 在
在![]() 上恒有意义
上恒有意义
即![]() 在
在![]() 上恒成立
上恒成立
令![]()
对称轴为![]() ,开口向上
,开口向上
当![]() 时,只需
时,只需![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]()
当![]() 时,只需
时,只需![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]()
当![]() 时, 只需
时, 只需![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]()
综上可知, ![]() 的取值范围为
的取值范围为![]()
(2)函数![]() 对称轴为
对称轴为![]()
由复合函数单调性的性质可知:
当![]() 时
时![]() 为单调递减函数,
为单调递减函数, ![]() 在
在![]() 上为单调递增函数,所以
上为单调递增函数,所以![]() 在
在![]() 上单调递减,不合题意
上单调递减,不合题意
当![]() 时,
时, ![]() 为单调递增函数, 若
为单调递增函数, 若![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上为单调递增函数.
上为单调递增函数.
所以由对称轴在![]() 左侧可得
左侧可得![]()
因为最大值为2,则![]()
即![]()
即![]() ,化简可得
,化简可得![]()
解得![]() 或
或 ![]()
因为![]()
所以![]()
当![]() 函数
函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]()


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨, ![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量, ![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(Ⅰ)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小;
的平均数与中位数的大小;
(Ⅱ)根据直方图估计利润![]() 不少于57万元的概率.
不少于57万元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷五《商功》中有如下叙述“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈“刍甍”指的是底面为矩形的对称型屋脊状的几何体,“下广三丈”是指底面矩形宽三丈,“袤四丈”是指底面矩形长四丈,“上袤二丈”是指脊长二丈,“无宽”是指脊无宽度,“高一丈”是指几何体的高为一丈.现有一个刍甍如图所示,下广三丈,袤四丈,上袤三丈,无广,高二丈,则该刍甍的外接球的表面积为_______________平方丈.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关,现收集了该种药用昆虫的6组观测数据如下表:
温度x/℃ | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得:
![]() ,
,![]() ,
,![]() 线性回归模型的残差平方和
线性回归模型的残差平方和![]() ,
,![]() ,
,
其中![]() 分别为观测数据中的温度和产卵数,
分别为观测数据中的温度和产卵数,![]()
(1)若用线性回归模型,求y关于x的回归方程![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求得y关于x的回归方程为![]() ,且相关指数
,且相关指数![]() .
.
①试与1中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为35℃时该用哪种药用昆虫的产卵数(结果取整数)
附:一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为 ,
,![]() ;相关指数
;相关指数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是指交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念性指数值,记交通指数为![]() ,其范围为
,其范围为![]() ,分别有五个级别:
,分别有五个级别:![]() ,畅通;
,畅通;![]() ,基本畅通;
,基本畅通;![]() ,轻度拥堵;
,轻度拥堵;![]() ,中度拥堵;
,中度拥堵;![]() ,严重拥堵.在晚高峰时段(
,严重拥堵.在晚高峰时段(![]() ),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的频率分布直方图如图所示.
),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的频率分布直方图如图所示.
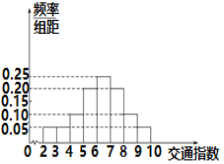
(1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数;
(2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽取的6个路段中任取2个,求至少有1个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.设不经过焦点
的左、右焦点.设不经过焦点![]() 的直线
的直线![]() 与椭圆交于两个不同的点
与椭圆交于两个不同的点![]() 、
、![]() ,焦点
,焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .若直线
.若直线![]() 、
、![]() 、
、![]() 的斜率依次成等差数列,求
的斜率依次成等差数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com