
【题目】正三棱柱![]() 的底边长为2,
的底边长为2, ![]() 分别为
分别为![]() 的中点.
的中点.
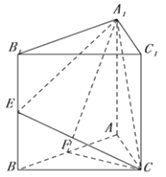
(1)已知![]() 为线段
为线段![]() 上的点,且
上的点,且![]() ,求证:
,求证: ![]() 面
面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(I)取B1A1中点为N,连结BN,推导出BN∥A1F,从而EM∥BN,进而EM∥A1F,由此能证明EM∥面A1FC.
(II)以F为坐标原点建立空间直角坐标系,设AA1=a,利用向量法能求出结果.
试题解析:
证明:(1)取![]() 中点为N,连结BN
中点为N,连结BN

则BN∥![]() F,又
F,又![]() =4
=4![]() M,
M,
则EM∥BN,所以EM∥![]() F,
F,
因为EM面![]() FC,
FC, ![]() F面
F面![]() FC,
FC,
故EM∥面![]() FC.
FC.
(2)如图,以F为坐标原点建立空间直角坐标系,设A![]() =a.
=a.
则F(0,0,0), ![]() (1,0,a),E(1,0,a2),C(0,
(1,0,a),E(1,0,a2),C(0, ![]() ,0),
,0),
![]() (1,
(1, ![]() ,
,![]() ),
),![]() (0,
(0, ![]() ,0),
,0), ![]() (2,0,
(2,0, ![]() ),
),![]() (1,
(1, ![]() ,a),
,a),
设平面![]() CF法向量为
CF法向量为![]() ,
,
设平面![]() EF法向量为
EF法向量为![]()
则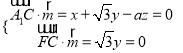 ,取z=1,得
,取z=1,得![]() =(a,0,1),
=(a,0,1),
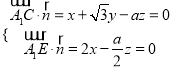 ,取x=1,得
,取x=1,得![]() =(a,
=(a, ![]() a,4);
a,4);
设二面角E![]() CF的平面角为θ,
CF的平面角为θ,
∵二面角E![]() CF所成角的余弦值为
CF所成角的余弦值为![]() ,
,
所以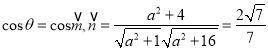
解得![]()
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() 上,
上, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]()
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于不同的四个点
交于不同的四个点![]() ,求四边形
,求四边形![]() 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率.
(2)在该样品的一等品中,随机抽取2件产品, ①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,4],则函数g(x)= ![]() 的定义域是( )
的定义域是( )
A.[0,2]
B.[0,2)
C.[0,1)∪(1,2]
D.[0,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床位每天的租金)不超过10元时,床位可以全部租出;当床位高于10元时,每提高1元,将有3张床位空闲. 为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入):
(1)把y表示成x的函数;
(2)试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.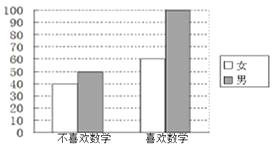
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求实数a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com