
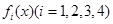 关于时间
关于时间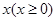 的函数关系式分别为
的函数关系式分别为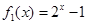 ,
,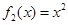 ,
,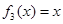 ,
,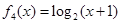 ,有以下结论:
,有以下结论: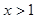 时,甲走在最前面;
时,甲走在最前面;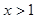 时,乙走在最前面;
时,乙走在最前面;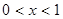 时,丁走在最前面,当
时,丁走在最前面,当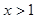 时,丁走在最后面;
时,丁走在最后面;科目:高中数学 来源:不详 题型:解答题
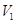 .
. 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
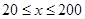 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.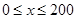 时,求函数
时,求函数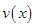 的表达式;
的表达式;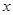 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)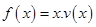 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com