
【题目】已知函数f(x)= 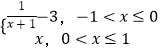 ,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 .
,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 .
【答案】( ![]() ,﹣2]∪(0,
,﹣2]∪(0,![]() ]
]
【解析】解:由g(x)=f(x)﹣mx﹣m=0,即f(x)=m(x+1),
分别作出函数f(x)和y=h(x)=m(x+1)的图象如图:
由图象可知f(1)=1,h(x)表示过定点A(﹣1,0)的直线,
当h(x)过(1,1)时,m= ![]() ,此时两个函数有两个交点,
,此时两个函数有两个交点,
此时满足条件的m的取值范围是0<m≤ ![]() ,
,
当h(x)过(0,﹣2)时,h(0)=﹣2,解得m=﹣2,此时两个函数有两个交点,
当h(x)与f(x)相切时,两个函数只有一个交点,此时 ![]() x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
当m=0时,只有1解,当m≠0,由△=9+4m=0得m=﹣ ![]() ,此时直线和f(x)相切,
,此时直线和f(x)相切,
∴要使函数有两个零点,则﹣ ![]() <m≤﹣2或0<m≤
<m≤﹣2或0<m≤ ![]() .
.
所以答案是:( ![]() ,﹣2]∪(0,
,﹣2]∪(0, ![]() ].
].



科目:高中数学 来源: 题型:
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一些数据,如下表所示:
x/0.01% | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)作出散点图,你能从散点图中发现含碳量与冶炼时间的一般规律吗?
(2)求回归直线方程.
(3)预测当钢水含碳量为160时,应冶炼多少分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游乐园的摩天轮最高点距离地面108米,直径长是98米,均速旋转一圈需要18分钟.如果某人从摩天轮的最低点![]() 处登上摩天轮并开始计时,那么:
处登上摩天轮并开始计时,那么:

(1)当此人第四次距离地面![]() 米时用了多少分钟?
米时用了多少分钟?
(2)当此人距离地面不低于![]() 米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌?
米时可以看到游乐园的全貌,求摩天轮旋转一圈中有多少分钟可以看到游乐园的全貌?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ ![]() x2﹣x+a,a∈R
x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1 , x2 , 且x1<x2 . (ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1x ![]() 恒成立,求正实数λ的取值范围.
恒成立,求正实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,其中
,其中![]() 为奇函数,
为奇函数, ![]() 为偶函数,若不等式
为偶函数,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的图象和直线
的图象和直线![]() 无交点,给出下列结论:
无交点,给出下列结论:
①方程![]() 一定没有实数根;
一定没有实数根;
②若![]() ,则必存在实数
,则必存在实数![]() ,使
,使![]() ;
;
③若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
④函数![]() 的图象与直线
的图象与直线![]() 也一定没有交点.
也一定没有交点.
其中正确的结论个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆. 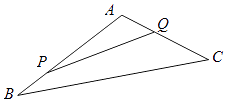
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,AP段围墙造价为每平方米150元,AQ段围墙造价为每平方米100元.若围围墙用了30000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com