
分析 先求出公差d=$\frac{1}{4}$($\frac{1}{{a}_{7}+1}$-$\frac{1}{{a}_{3}+1}$)=$\frac{1}{24}$,再求出$\frac{1}{{a}_{19}+1}$,由此能求出a19的值.
解答 解:∵数列{an}中,a3=2,a7=1,$\{\frac{1}{{{a_n}+1}}\}$为等差数列,
∴d=$\frac{1}{4}$($\frac{1}{{a}_{7}+1}$-$\frac{1}{{a}_{3}+1}$)=$\frac{1}{4}$($\frac{1}{2}-\frac{1}{3}$)=$\frac{1}{24}$,
∴$\frac{1}{{a}_{19}+1}$=$\frac{1}{{a}_{3}+1}$+16d=$\frac{1}{3}+16×\frac{1}{24}$=1,
解得a19=0.
故答案为:0.
点评 本题考查等差数列中两项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
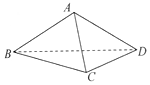 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )| A. |  | B. | 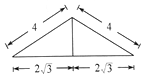 | C. | 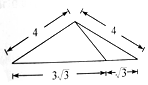 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{{{cos}^2}x}}$ | B. | $-\frac{1}{{{{cos}^2}x}}$ | C. | $\frac{cos2x}{{{{cos}^2}x}}$ | D. | $-\frac{cos2x}{{{{cos}^2}x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 40 | C. | 50 | D. | 以上都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com